Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
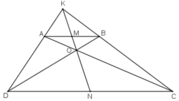
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒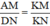 
(Hệ quả định lý Ta-let)
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒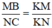 
(Hệ quả định lý Ta-let)
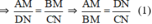
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒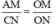 
(Hệ quả định lý Ta-let)
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒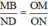 
(Hệ quả định lý Ta-let)
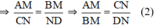
Từ (1) và (2) suy ra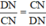 
⇒ CN = DN ⇒ AM = MB
Vậy M, N là trung điểm AB, CD.
Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = KN/KO và BN/FO = KM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = KO/KM
và FO/CM = KO/KM ⇒EO/DM=FO/CM ⇒ DM=CM suy ra đường thẳng OK đi qua trung điểm của các cạnh AB và CD.
Bài 2:
Xét ΔADC có OM//DC
nen OM/DC=AM/AD(1)
Xét ΔBDC có ON//DC
nên ON/DC=BN/BC(2)
Xét hình thag ABCD có MN//AB//CD
nên AM/AD=BN/BC(3)
Từ (1) (2)và (3) suy ra OM=ON
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒ \(\frac{AM}{DN}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒ \(\frac{MB}{NC}=\frac{KM}{KN}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{DN}=\frac{BM}{CN}\Rightarrow\frac{AM}{BM}=\frac{DN}{CN}\left(1\right)\)
.ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒ \(\frac{AM}{CN}=\frac{ON}{CN}\)( hệ quả của định lí Talet )
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒ \(\frac{MB}{ND}=\frac{OM}{ON}\)( hệ quả của định lí Talet )
\(\Rightarrow\frac{AM}{CN}=\frac{BM}{ND}\Rightarrow\frac{AM}{BM}=\frac{CN}{DN}\left(2\right)\)
Từ (1)(2) , suy ra :
\(\frac{DN}{CN}=\frac{CN}{DN}\Rightarrow CN=DN\Rightarrow AM=MB\)
Vậy M, N là trung điểm AB, CD.
a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)(hai góc so le trong, AB//CD)
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
Do đó: ΔOAB\(\sim\)ΔOCD
=>\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
=>\(\dfrac{OC}{OA}=\dfrac{OD}{OB}\)
=>\(\dfrac{OC}{OA}+1=\dfrac{OD}{OB}+1\)
=>\(\dfrac{OC+OA}{OA}=\dfrac{OD+OB}{OB}\)
=>\(\dfrac{AC}{OA}=\dfrac{BD}{OB}\)
=>\(\dfrac{OA}{AC}=\dfrac{OB}{BD}\)(2)
b: Xét ΔCAD có OE//AD
nên \(\dfrac{DE}{DC}=\dfrac{AO}{AC}\)(1)
Xét ΔBDC có OF//BC
nên \(\dfrac{CF}{CD}=\dfrac{BO}{BD}\left(3\right)\)
Từ (1),(2),(3) suy ra \(\dfrac{DE}{DC}=\dfrac{CF}{CD}\)
=>DE=CF