Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 1:
Áp dụng định lý Talet cho $EO\parallel DC$:
$\frac{OE}{DC}=\frac{AO}{AC}(1)$
Áp dụng định lý Talet cho $OF\parallel DC$:
$\frac{OF}{DC}=\frac{OB}{BD}(2)$
Áp dụng định lý Talet cho $AB\parallel CD$:
$\frac{OA}{OC}=\frac{OB}{OD}\Leftrightarrow \frac{OA}{OA+OC}=\frac{OB}{OB+OD}\Leftrightarrow \frac{OA}{AC}=\frac{OB}{BD}(3)$
Từ $(1);(2);(3)\Rightarrow \frac{OE}{DC}=\frac{OF}{DC}$
$\Rightarrow OE=OF$ (đpcm)
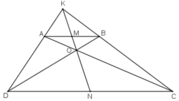
Gọi KO cắt AB, CD lần lượt tại M, N.
ΔKDN có AM // DN (A ∈ KD, M ∈ KN) ⇒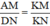 
(Hệ quả định lý Ta-let)
ΔKCN có BM // CN (M ∈ KN, B ∈ KC) ⇒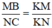 
(Hệ quả định lý Ta-let)
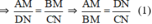
ΔOCN có AM // NC (A ∈ OC, M ∈ ON) ⇒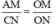 
(Hệ quả định lý Ta-let)
ΔODN có MB // ND (M ∈ ON, B ∈ OD) ⇒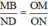 
(Hệ quả định lý Ta-let)
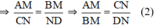
Từ (1) và (2) suy ra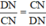 
⇒ CN = DN ⇒ AM = MB
Vậy M, N là trung điểm AB, CD.
Ta có EO//DC ⇒ OE/DC = AO/AC (1)
OF//DC ⇒ OF/DC = BO/BD (2)
Ta có: AB//DC ⇒ OA/OC = OB/OD
⇒ OA/ (OC + OA) = OB/(OD+ OB) ⇒ OA/AC = OB/BD (3)
Từ (1),(2),(3) ta có OE/DC = OF/DC ⇒ OE = OF
Ta có AB//EF
⇒ AN/EO = KN/KO và BN/FO = KM/KO
⇒ AN/EO = BN/FO ⇒ AN = BN
Tương tự: FE//DC ⇒ EO/DM = KO/KM
và FO/CM = KO/KM ⇒EO/DM=FO/CM ⇒ DM=CM
Vì OE // DC ==> OA/AC = OE/DC (định lý Ta-let) (1)
Vì OF // DC ==> OB/BD = OF/DC (định lý Ta-let) (2)
Vì AB // CD ==> OA/OC = OB/OD (định lý ta-let)
Theo tính chất dãy tỉ số bằng nhau ta có:
OA/OC = OB/OD <=> OA / (OA + OC) = OB / (OB + OD)
<=> OA / AC = OB / BD (3)
Từ (1), (2) và (3) suy ra ta có:
OE / DC = OF / DC <=> OE = OF (đpcm)
bạn có thể giải rõ hơn giùm mình