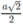Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có thể chia được nhiều nhất là 2 đội vì UCLN(16;14;40)=2

Lời giải:
Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
2.Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)

Cho hàm số y = f(x) liên tục trên [a; b].
F(x) là một nguyên hàm của f(x) trên [a; b].
Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x)
Kí hiệu là 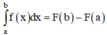

Gọi độ dài của ba đoạn thẳng đã cho là a. Khi đó các đầu mút của chúng là đỉnh của một hình tám mặt đều, mỗi mặt là tam giác đều có cạnh bằng