Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

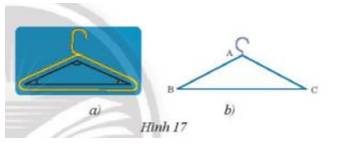
a: BC=10cm
C=AB+BC+AC=6+8+10=24(cm)
b: Xét ΔABD vuông tại A và ΔHBD vuông tại H có
BD chung
\(\widehat{ABD}=\widehat{HBD}\)
Do đó: ΔABD=ΔHBD
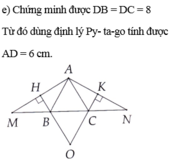
c: Ta có: ΔABD=ΔHBD
nên DA=DH
mà DH<DC
nên DA<DC

à làm thêm câu b):
Vì \(\Delta\text{ABC}=\Delta\text{MNP}\)nên:
AB=MN=5cm; AC=MP=7cm và BC=NP.
Trong tam giác ABC có:
AB+BC+CA=22 (cm)
=> 5 + BC + 7 = 22
=> BC = 22 - 5 - 7
=> BC = 10 (cm)
Mà BC = NP = 10 cm
Vậy...(bạn viết tương tự nhé).

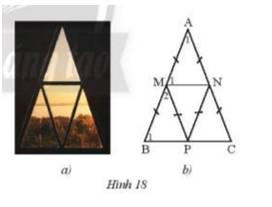
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau

a) Gọi độ dài cạnh cần tìm là x (cm) (x > 0)
Theo hệ quả của bất đẳng thức tam giác, ta có:
13 - 6 < x < 13 + 6
7 < x < 19
Do tam giác cân nên x = 13 (cm)
b) Chu vi tam giác cân đó:
6 + 13 + 13 = 32 (cm)

Xét ΔABC = ΔXYZ có
\(\widehat{A}=\widehat{X}=35^0\\ \widehat{B}=\widehat{Y}\\ \widehat{C}=\widehat{Z}=80^0\)
Xét ΔABC có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\\ \Rightarrow\widehat{B}=\widehat{Y}=180^0-\widehat{A}-\widehat{B}\\ =180^0-35^0-80^0\\ =65^0\)


Vì tam giác ABC cân tại A
\( \Rightarrow \) AB = AC = 20 cm
\( \Rightarrow \) Chu vi tam giác ABC = AB + AC + BC = 20 + 20 + 28 = 68 cm
Vì \(\Delta ABC \) cân tại A \( \Rightarrow \widehat B = \widehat C\) = 35°
Mà tổng 3 góc trong một tam giác là 180°
\( \Rightarrow \widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {35^o} - {35^o} = {110^o}\)