NT
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
KT
13 tháng 1 2019
\(\left(3x-2\right)\left(x+1\right)^2\left(3x+8\right)=-16\)
<=> \(\left(3x-2\right)\left(x+1\right)^2.3^2.\left(3x+8\right)+144=0\)
<=> \(\left(3x-2\right)\left(3x+3\right)^2\left(3x+8\right)+144=0\) (*)
Đặt \(3x+3=t\) Khi đó pt (*) trở thành:
\(\left(t-5\right)t^2\left(t+5\right)+144=0\)
<=> \(t^4-25t^2+144=0\)
<=> \(\left(t-4\right)\left(t-3\right)\left(t+3\right)\left(t+4\right)=0\)
đến đây bn tự giải tiếp nhé
21 tháng 3 2021
a)(2x+1)(3x-2)=(5x-8)(2x+1)
⇔(2x+1)(3x-2)-(5x-8)(2x+1)=0
⇔(2x+1)(3x-2-5x+8)=0
⇔(2x+1)(-2x+6)=0
⇔2x+1=0 hoặc -2x+6=0
1.2x+1=0⇔2x=-1⇔x=-1/2
2.-2x+6=0⇔-2x=-6⇔x=3
phương trình có 2 nghiệm x=-1/2 và x=3
ND
19 tháng 3 2020
Bạn bạn nhân phân phối (3x-1)(x-2) và (3x-1)(7x-10)
Sau đó chuyển vế sao cho về phương trình bậc 2
Sau đó giải pt bậc hai là ra
19 tháng 3 2020
Ta có : (3x -1 ) . ( x + 2 ) = ( 3x-1 ) .( 7x - 10)
<=>3.x2 + 6x -x -2 = 21x2 -30x - 7x +10
<=> 3x2 + 5x -2 = 21x2 -37x + 10
<=> 3x2 +5x - 3 - 21x2 +37x -10 = 0
<=> -18x2 + 42x -12 = 0
<=> 3x2 -7x +2 = 0
<=> 3x2 -x -6x + 2 = 0
<=> x. ( 3x -1 ) -2.(3x -1 ) = 0
<=> (3x -1 ) . ( x - 2 ) = 0
<=> \(\orbr{\begin{cases}3x-1=0\\x-2=0\end{cases}}\)
<=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}\)
Tập nghiệm của phương trình là : { \(\frac{1}{3}\); 2}
28 tháng 5 2017
a) (x-1)(5x+3)=(3x-8)(x-1)
= (x-1)(5x+3)-(3x-8)(x-1)=0
=(x-1)[(5x+3)-(3x-8)]=0
=(x-1)(5x+3-3x+8)=0
=(x-1)(2x+11)=0
\(\Leftrightarrow\) x-1=0 hoặc 2x+11=0
\(\Leftrightarrow\) x=1 hoặc x=\(\dfrac{-11}{2}\)
Vậy S={1;\(\dfrac{-11}{2}\)}
b) 3x(25x+15)-35(5x+3)=0
=3x.5(5x+3)-35(5x+3)=0
=15x(5x+3)-35(5x+3)=0
=(5x+3)(15x-35)=0
\(\Leftrightarrow\) 5x+3=0 hoặc 15x-35=0
\(\Leftrightarrow\) x=\(\dfrac{-3}{5}\) hoặc x=\(\dfrac{7}{3}\)
Vậy S={\(\dfrac{-3}{5};\dfrac{7}{3}\)}
c) (2-3x)(x+11)=(3x-2)(2-5x)
=(2-3x)(x+11)-(3x-2)(2-5x)=0
=(3x-2)[(x+11)-(2-5x)]=0
=(3x-2)(x+11-2+5x)=0
=(3x-2)(6x+9)=0
\(\Leftrightarrow\) 3x-2=0 hoặc 6x+9=0
\(\Leftrightarrow\) x=\(\dfrac{2}{3}\) hoặc x=\(\dfrac{-3}{2}\)
Vậy S={\(\dfrac{2}{3};\dfrac{-3}{2}\)}
d) (2x2+1)(4x-3)=(2x2+1)(x-12)
=(2x2+1)(4x-3)-(2x2+1)(x-12)=0
=(2x2+1)[(4x-3)-(x-12)=0
=(2x2+1)(4x-3-x+12)=0
=(2x2+1)(3x+9)=0
\(\Leftrightarrow\)2x2+1=0 hoặc 3x+9=0
\(\Leftrightarrow\)x=\(\dfrac{1}{2}\)hoặc x=\(\dfrac{-1}{2}\) hoặc x=-3
Vậy S={\(\dfrac{1}{2};\dfrac{-1}{2};-3\)}
e) (2x-1)2+(2-x)(2x-1)=0
=(2x-1)[(2x-1)+(2-x)=0
=(2x-1)(2x-1+2-x)=0
=(2x-1)(x+1)=0
\(\Leftrightarrow\) 2x-1=0 hoặc x+1=0
\(\Leftrightarrow\) x=\(\dfrac{-1}{2}\) hoặc x=-1
Vậy S={\(\dfrac{-1}{2}\);-1}
f)(x+2)(3-4x)=x2+4x+4
=(x+2)(3-4x)=(x+2)2
=(x+2)(3-4x)-(x+2)2=0
=(x+2)[(3-4x)-(x+2)]=0
=(x+2)(3-4x-x-2)=0
=(x+2)(-5x+1)=0
\(\Leftrightarrow\) x+2=0 hoặc -5x+1=0
\(\Leftrightarrow\) x=-2 hoặc x=\(\dfrac{1}{5}\)
Vậy S={-2;\(\dfrac{1}{5}\)}
S
7 tháng 1 2019
\(\frac{\left(3x+1\right)\left(3x-2\right)}{3}+5\left(3x+1\right)=\frac{2\left(2x+1\right)\left(3x+1\right)}{3}+2\left(3x+1\right)\)
\(\Leftrightarrow\frac{2\left(2x+1\right)\left(3x+1\right)-\left(3x+1\right)\left(3x-2\right)}{3}-3\left(3x+1\right)=0\)
\(\Leftrightarrow\frac{\left(4x+2\right)\left(3x+1\right)-\left(3x+1\right)\left(3x-2\right)}{3}-3\left(3x+1\right)=0\)
\(\Leftrightarrow\frac{12x^2+10x+2-9x^2+6x-3x+2}{3}-9x-3=0\)
\(\Leftrightarrow\frac{3x^2+13x+4-27x-9}{3}=0\Leftrightarrow\frac{3x^2-14x-5}{3}=0\)
\(\Leftrightarrow3x^2-14x-5=0\Leftrightarrow3x^2-14x=5\Leftrightarrow x\left(3x-14\right)=5\)
\(.................\)
AK
7 tháng 1 2019
v: Làm tiếp nè
3x^2 - 14x - 5 = 0
<=> 3x^2 - 15x + x - 5 = 0
<=> ....
AT
19 tháng 3 2020
( 3x - 1)( x + 2) = ( 3x - 1)(7x - 10)
<=>( 3x - 1)( x + 2) - ( 3x - 1)(7x - 10) = 0
<=> ( 3x - 1)( x + 2 - 7x + 10) = 0
<=>( 3x - 1)( -6x + 12) = 0
\(\Leftrightarrow\orbr{\begin{cases}3x-1=0\\-6x+12=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}}\)
Vậy.....
19 tháng 3 2020
\(\left(3x-1\right)\left(x+2\right)=\left(3x-1\right)\left(7x-10\right)\)
\(3x^2+5x-2=21x^2-37x+10\)
\(3x^2+5x-2-21x^2+37x-10=0\)
\(-18x^2+42x-12=0\)
\(-6\left(3x-1\right)\left(x-2\right)=0\)
\(-6\ne0\)
\(\left(3x-1\right)\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x=1\\x=2\end{cases}\Rightarrow\orbr{\begin{cases}x=\frac{1}{3}\\x=2\end{cases}}}\)
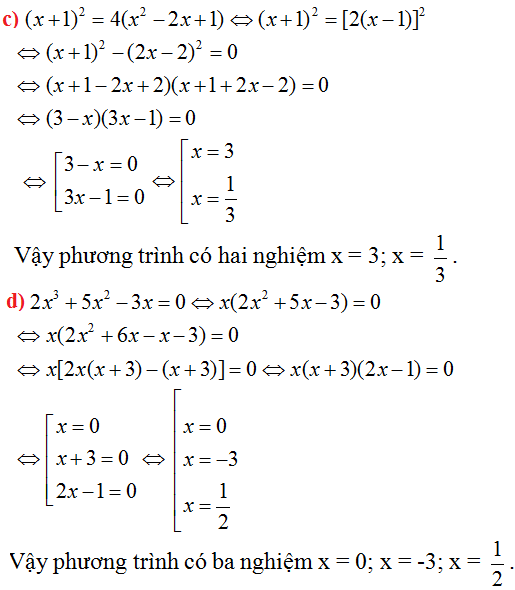
\(\left(3x-2\right)\left(x+1\right)^2\left(3x+8\right)=-16\)
\(\Leftrightarrow\left[\left(3x-2\right)\left(3x+8\right)\right]\left[9\left(x+1\right)^2\right]=-16.9\)
\(\Leftrightarrow\left(9x^2+18x-16\right)\left(9x^2+18x+9\right)=-144\)
\(\Leftrightarrow\left(9x^2+18x\right)^2-7\left(9x^2+18x\right)-144=-144\)
\(\Leftrightarrow\left(9x^2+18x\right)^2-7\left(9x^2+18x\right)=0\)
\(\Leftrightarrow\left(9x^2+18x\right)\left(9x^2+18x-7\right)=0\)
\(\Leftrightarrow9x\left(x+2\right)\left(3x-1\right)\left(3x+7\right)=0\)
Tập nghiệm của pt là: \(S=\left\{0;-2;\frac{1}{3};\frac{-7}{3}\right\}\)
\(\left(3x-2\right)\left(x-1\right)^2\left(3x+8\right)=-16\)
\(\Leftrightarrow\left[\left(3x-2\right)\left(3x+8\right)\right]\left[9\left(x+1\right)^2\right]=-16.9=-144\)
\(\Leftrightarrow\left(9x^2+18x\right)^2-7\left(9x^2+18x\right)-144=-144\)
\(\Leftrightarrow\left(9x^2+18x\right)^2-7\left(9x^2+18x\right)=0\)
\(\Leftrightarrow\left(9x^2+18x\right)\left(9x^2+18x-7\right)=0\)
\(\Leftrightarrow9x\left(x+2\right)\left(3x-1\right)\left(3x+7\right)=0\)
Tập nghiệm của phương trình là : \(S=\left\{0;-2;\frac{1}{3};\frac{-7}{3}\right\}\)