Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đây là dạng toán nâng cao chuyên đề về so sánh phân số, cấu trúc thi chuyên, thi học sinh giỏi, thi violympic. Hôm nay olm sẽ hướng dẫn em cách giải dạng này như sau.
Xét dãy số: 2; 3; 4;...; 2023
Dãy số trên là dãy số cách đều với khoảng cách là: 2 - 1 = 1
Số số hạng của dãy số trên là: (2023 - 2) : 1 + 1 = 2022
Vì \(\dfrac{3}{2^2}\) = \(\dfrac{3}{4}\) < 1 ; \(\dfrac{8}{3^2}\) = \(\dfrac{3^2-1}{3^2}\) < 1;...; \(\dfrac{2023^2-1}{2023^2}\) < 1
Vậy A là tổng của 2022 phân số mã mỗi phân số đều nhỏ hơn 1
⇒ A < 1 x 2022 = 2022 (1)
Mặt khác ta có:
A = \(\dfrac{3}{2^2}\) + \(\dfrac{8}{3^2}\) + \(\dfrac{15}{4^2}\) + \(\dfrac{2023^2-1}{2023^2}\)
A = 1 - \(\dfrac{1}{2^2}\) + 1 - \(\dfrac{1}{3^2}\) + ... + 1 - \(\dfrac{1}{2023^2}\)
A = (1 + 1 + 1+ ...+ 1) - (\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\)+...+ \(\dfrac{1}{2023^2}\))
A = 2022 - (\(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + .... + \(\dfrac{1}{2023^2}\))
Đặt B = \(\dfrac{1}{2^2}\) + \(\dfrac{1}{3^2}\) + .... + \(\dfrac{1}{2023^2}\)
\(\dfrac{1}{2^2}\) < \(\dfrac{1}{1.2}\) = \(\dfrac{1}{1}\) - \(\dfrac{1}{2}\)
\(\dfrac{1}{3^2}\) < \(\dfrac{1}{2.3}\) = \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)
\(\dfrac{1}{4^2}\) < \(\dfrac{1}{3.4}\) = \(\dfrac{1}{3}\) - \(\dfrac{1}{4}\)
............................
\(\dfrac{1}{2023^2}\)< \(\dfrac{1}{2022.2023}\) = \(\dfrac{1}{2022}\) - \(\dfrac{1}{2023}\)
Cộng vế với vế ta có:
B < 1 - \(\dfrac{1}{2023}\)
⇒ - B > -1 + \(\dfrac{1}{2023}\)
⇒ A = 2022 - B > 2022 - 1 + \(\dfrac{1}{2023}\) = 2021 + \(\dfrac{1}{2023}\) ⇒ A > 2021 (2)
Kết hợp (1) và (2) ta có:
2021 < A < 2022
Vậy A không phải là số tự nhiên (đpcm)
A = 3. \(\dfrac{1}{1.2}\) - 5. \(\dfrac{1}{2.3}\) + 7. \(\dfrac{1}{3.4}\) + ... + 15. \(\dfrac{1}{7.8}\) -17 . \(\dfrac{1}{8.9}\)

Áp dụng tính chất phân phối, rồi tính giá trị biểu thức.
Chẳng hạn,
Với , thì
ĐS. ; C = 0.
Xem thêm tại: http://loigiaihay.com/bai-77-trang-39-phan-so-hoc-sgk-toan-6-tap-2-c41a5943.html#ixzz4eU1fQCGw

A= \(\dfrac{-3}{5}-\dfrac{-4}{5}+\dfrac{-9}{10}\)
A = \(\dfrac{-7}{10}\)

a) \(1-\dfrac{1}{2}=\dfrac{1}{2}\)
\(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{3-2}{6}=\dfrac{1}{6}\)
\(\dfrac{1}{3}-\dfrac{1}{4}=\dfrac{4-3}{12}=\dfrac{1}{12}\)
\(\dfrac{1}{4}-\dfrac{1}{5}=\dfrac{5-4}{20}=\dfrac{1}{20}\)
\(\dfrac{1}{5}-\dfrac{1}{6}=\dfrac{6-5}{30}=\dfrac{1}{30}\)
b) \(\dfrac{1}{2}+\dfrac{1}{6}+\dfrac{1}{12}+\dfrac{1}{20}+\dfrac{1}{30}\)
\(=\left(1-\dfrac{1}{2}\right)+\left(\dfrac{1}{2}-\dfrac{1}{3}\right)+\left(\dfrac{1}{3}-\dfrac{1}{4}\right)+\left(\dfrac{1}{4}-\dfrac{1}{5}\right)+\left(\dfrac{1}{5}+\dfrac{1}{6}\right)\)
\(=1+\left(-\dfrac{1}{2}+\dfrac{1}{2}\right)+\left(-\dfrac{1}{3}+\dfrac{1}{3}\right)+\left(-\dfrac{1}{4}+\dfrac{1}{4}\right)+\left(-\dfrac{1}{5}+\dfrac{1}{5}\right)+-\dfrac{1}{6}\)\(=1+-\dfrac{1}{6}\)
\(=\dfrac{5}{6}\)

a) \(\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{6}\right)\left(1-\dfrac{1}{10}\right)...\left(1-\dfrac{1}{780}\right)\)
\(=\dfrac{2}{3}.\dfrac{5}{6}.\dfrac{9}{10}.....\dfrac{779}{780}\)\(=\)

bài 1:
a) \(4\dfrac{1}{2}x:\dfrac{5}{12}=0,5\) ; b)\(1,5+1\dfrac{1}{4}x=\dfrac{2}{3}\)
\(\dfrac{9}{2}x:\dfrac{5}{12}=\dfrac{1}{2}\) \(\dfrac{3}{2}+\dfrac{5}{4}x=\dfrac{2}{3}\)
\(\dfrac{9}{2}x\) \(=\dfrac{1}{2}.\dfrac{5}{12}\) \(\dfrac{5}{4}x=\dfrac{2}{3}-\dfrac{3}{2}\)
\(\dfrac{9}{2}x\) \(=\dfrac{5}{24}\) \(\dfrac{5}{4}x=\dfrac{-5}{6}\)
\(x\) \(=\dfrac{5}{24}:\dfrac{9}{2}\) \(x=\dfrac{-5}{6}:\dfrac{5}{4}\)
\(x\) \(=\dfrac{5}{108}\) \(x=\dfrac{-2}{3}\)
c) Cho mình hỏi x ở đâu vậy ???
d)\(\left(x-5\right):\dfrac{1}{3}=\dfrac{2}{5}\) e)\(\left(4,5-2x\right):\dfrac{3}{4}=1\dfrac{1}{3}\)
\(\left(x-5\right)\) \(=\dfrac{2}{5}.\dfrac{1}{3}\) \(\left(\dfrac{9}{2}-2x\right):\dfrac{3}{4}=\dfrac{4}{3}\)
\(x-5\) \(=\dfrac{2}{15}\) \(\dfrac{9}{2}-2x\) =\(\dfrac{4}{3}.\dfrac{3}{4}\)
\(x\) \(=\dfrac{2}{15}+5\) \(\dfrac{9}{2}-2x=1\)
\(x\) \(=\dfrac{77}{15}\) \(2x=\dfrac{9}{2}-1\)
f) \(\left(2,7x-1\dfrac{1}{2}x\right):\dfrac{2}{7}=\dfrac{-21}{7}\) \(2x=\dfrac{7}{2}\)
\(\left(\dfrac{27}{10}x-\dfrac{3}{2}x\right):\dfrac{2}{7}=-3\) \(x=\dfrac{7}{2}:2\)
\(\left[x\left(\dfrac{27}{10}-\dfrac{3}{2}\right)\right]=-3.\dfrac{2}{7}\) \(x=\dfrac{7}{4}\)
\(x.\dfrac{6}{5}=\dfrac{-6}{7}\)
\(x=\dfrac{-6}{7}:\dfrac{6}{5}\)
\(x=\dfrac{-5}{7}\)
bài 2:
Theo bài ra ta có :\(\dfrac{a}{27}=\dfrac{-5}{9}=\dfrac{-45}{b}\)
\(\Rightarrow9a=27.\left(-5\right)\Rightarrow a=\dfrac{27.\left(-5\right)}{9}=-15\)
\(\Rightarrow\left(-5\right)b=\left(-45\right).9\Rightarrow b=\dfrac{\left(-45\right).9}{-5}=81\)
Vậy \(a=-15;b=81\)

1/
a) ta có \(\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{97.100}=\dfrac{1}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{97.100}\right)\)
\(=\dfrac{1}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{3}.\dfrac{99}{100}=\dfrac{33}{100}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33x}{2009}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33}{2009}.x\Rightarrow x=\dfrac{33}{100}:\dfrac{0,33}{2009}=2009\)
b,1 + 1/3 + 1/6 + 1/10 + ... + 2/x(x+1)=1 1991/1993
2 + 2/6 + 2/12 + 2/20 + ... + 2/x(x+1) = 3984/1993
2.(1/1.2 + 1/2.3 + 1/3.4 + ... + 1/x(x+1) = 3984/1993
2.(1 − 1/2 + 1/2 − 1/3 + ... + 1/x − 1/x+1)=3984/1993
2.(1 − 1/x+1) = 3984/1993
1 − 1/x + 1= 3984/1993 :2
1 − 1/x+1 = 1992/1993
1/x+1 = 1 − 1992/1993
1/x+1=1/1993
<=>x+1 = 1993
<=>x+1=1993
<=> x+1=1993
<=> x = 1993-1
<=> x = 1992
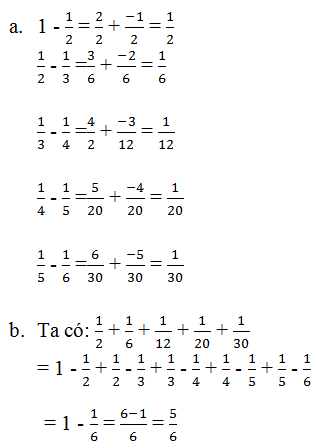
A = \(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2022}-\dfrac{1}{2023}\)
= \(1-\dfrac{1}{2023}\)
= \(\dfrac{2022}{2023}\)