
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

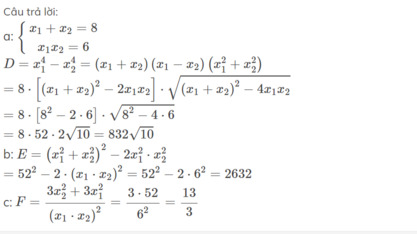

a: \(\left\{{}\begin{matrix}x_1+x_2=8\\x_1x_2=6\end{matrix}\right.\)
\(D=x_1^4-x_2^4=\left(x_1+x_2\right)\left(x_1-x_2\right)\left(x_1^2+x_2^2\right)\)
\(=8\cdot\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\cdot\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}\)
\(=8\cdot\left[8^2-2\cdot6\right]\cdot\sqrt{8^2-4\cdot6}\)
\(=8\cdot52\cdot2\sqrt{10}=832\sqrt{10}\)
b: \(E=\left(x_1^2+x_2^2\right)^2-2x_1^2\cdot x_2^2\)
\(=52^2-2\cdot\left(x_1\cdot x_2\right)^2=52^2-2\cdot6^2=2632\)
c: \(F=\dfrac{3x_2^2+3x_1^2}{\left(x_1\cdot x_2\right)^2}=\dfrac{3\cdot52}{6^2}=\dfrac{13}{3}\)

Ta có \(\Delta'=b'^2-ac=\left(-3\right)^2-m=9-m\)
Để phương trình trên có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow9-m\ge0\Leftrightarrow m\le9\)
Áp dụng Viet, ta có: \(\left\{{}\begin{matrix}x_1+x_2=-\frac{b}{a}=6\\x_1x_2=m\end{matrix}\right.\)
a) Ta có:
\(x_1^2+x_2^2=36\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=36\\ \Leftrightarrow6^2-2m=36\Leftrightarrow2m=0\Leftrightarrow m=0\left(tm\right)\)
b) Ta có:
\(\frac{1}{x_1}+\frac{1}{x_2}=3\Leftrightarrow\frac{x_2+x_1}{x_1x_2}=3\Leftrightarrow\frac{6}{m}=3\Leftrightarrow m=2\left(tm\right)\)
c) Ta có:
\(\left\{{}\begin{matrix}x_1+x_2=6\\x_1-x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_1=10\\x_1-x_2=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=5\\x_2=x_1-4=5-4=1\end{matrix}\right.\)
Thay x1; x2 vào x1x2=m, ta có:
\(5\cdot1=m\Leftrightarrow m=5\left(tm\right)\)

a: Thay x=2 vào pt, ta được:
\(-3\cdot4-5\cdot2-m+2=0\)
=>-m-20=0
hay m=-20
b: Để phương trình có hai nghiệm trái dấu thì -3(-m+2)<0
=>-m+2>0
hay m<2
c: Để phương trình có hai nghiệm cùng âm thì \(\left\{{}\begin{matrix}\left(-5\right)^2-4\cdot\left(-3\right)\left(-m+2\right)>=0\\\dfrac{-m+2}{-3}>0\\\dfrac{5}{-3}< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}25+12\left(-m+2\right)>=0\\-m+2< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}25-12m+24>=0\\-m< -2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< =\dfrac{49}{12}\\m>2\end{matrix}\right.\Leftrightarrow2< m\le\dfrac{49}{12}\)

Theo định lí Vi-et , ta có : \(\begin{cases}x_1+x_2=1\\x_1.x_2=-5\end{cases}\)

Theo hệ thức Viet ta có: \(\left\{{}\begin{matrix}x_1+x_2=\frac{-2\left(m-4\right)}{m-2}\\x_1x_2=\frac{m-4}{m-2}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2=\frac{-2\left(m-4\right)}{m-2}\\2x_1x_2=\frac{2\left(m-4\right)}{m-2}\end{matrix}\right.\)
\(\Rightarrow x_1+x_2+2x_1x_2=0\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m