Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) F = \(F_{13}+F_{23}=\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-8}}{0,03^2}+\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-58}}{0.03^2}=0.128\left(N\right)\)
b) F = \(F_{13}+F_{23}=\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-8}}{0,04^2}+\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-8}}{0,02^2}=0,18\left(N\right)\)
c) F = \(\left|F_{13}-F_{23}\right|=\left|\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-8}}{0,04^2}-\frac{k\cdot8\cdot10^{-8}\cdot8\cdot10^{-8}}{0,1^2}\right|=0,03024\left(N\right)\)
d) F = \(\sqrt{F_{13}^2+F^2_{23}+2\cdot F_{13}\cdot F_{23}\cdot\cos60}=0,0277\left(N\right)\)

1/
CA=4cm; CB=10 cm
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\)
\(\Rightarrow\sum F=\left|F_1-F_2\right|=...\left(N\right)\)
AC=CB=5cm
\(AB^2=AC^2+BC^2-2.AC.BC.\cos\alpha\Rightarrow\alpha=....\)
\(F_1=\dfrac{k\left|q_1q_3\right|}{AC^2}\left(N\right);F_2=\dfrac{k\left|q_2q_3\right|}{BC^2}\left(N\right)\)
\(\sum F=\sqrt{F_1^2+F_2^2+2.F_1F_2.\cos\left(180^0-\alpha\right)}=...\left(N\right)\)

Vì C cách đều A và B nên C nằm trên đường trung trực của AB
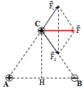
F → = F → 1 + F → 2 → F 1 = k q 1 q 3 A C 2 = 23 , 04.10 − 3 N F 2 = k q 2 q 3 B C 2 = 23 , 04.10 − 3 N → F 1 = F 2 → F → ⊥ C H
F = 2 F 1 cos F → 1 ; F → = 2 F 1 cos C A B ^ = 2 F 1 A H A C = 27 , 65.10 − 3 N

Đáp án A
Dùng phương pháp số phức tổng hợp lực (chọn trục nằm ngang làm trục chuẩn):
F → = F → A C + F → B C = F A C ∠ π 2 + F B C < 0
= 3 , 75 ∠ π 2 + 5 , 625 = 15 13 8 ∠ 0 , 588 N

bc cũng vậy chỉ khác r và q