Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
![]()
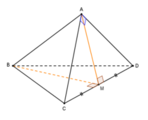
nên ∆ BCDlà tam giác đều.
![]()
nên theo định lý Py-ta-go đảo, ta có ∆ ACD vuông cân tại A .
Khi đó, gọi M là trung điểm CD thì: AM ⊥ CD và BM ⊥ CD Ta có:
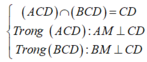
![]()
∆
BCD đều có đường cao
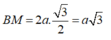
∆
ACD vuông cân tại A nên trung tuyến
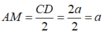
Áp dụng định lý hàm cos trong
∆
AMB, ta có:
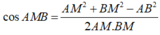
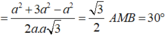
![]()
Vậy góc giữa hai mặt phẳng (ACD) và (BCD) có số đo bằng 30 o


Từ C hạ \(CK\perp BD\Rightarrow CK\perp\left(ABD\right)\Rightarrow CK\perp AD\)
Mà \(AD\) không vuông góc với \(\left(BCD\right)\)
\(\Rightarrow CH\perp AD\Leftrightarrow H\equiv K\)
\(\Rightarrow H\) là chân đường vuông góc hạ từ C xuống BD
Theo hệ thức lượng: \(BH.BD=BC^2\Rightarrow BH=\frac{BC^2}{BD}=\frac{BC^2}{\sqrt{BC^2+CD^2}}=...\)

a.
Do \(AB=AC\Rightarrow\Delta ABC\) cân tại A
\(\Rightarrow AM\) là trung tuyến đồng thời là đường cao
\(\Rightarrow AM\perp BC\) (1)
Mà \(\left\{{}\begin{matrix}AD\perp AB\left(gt\right)\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABC\right)\Rightarrow AD\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(ADM\right)\)
b.
Từ A kẻ \(AE\perp DM\) (E thuộc DM)
Do \(BC\perp\left(ADM\right)\Rightarrow BC\perp AE\)
\(\Rightarrow AE\perp\left(BCD\right)\Rightarrow AE=d\left(A;\left(BCD\right)\right)\)
\(BC=\sqrt{AB^2+AC^2}=5\sqrt{2}\Rightarrow AM=\dfrac{1}{2}BC=\dfrac{5\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông ADM:
\(AE=\dfrac{AD.AM}{\sqrt{AD^2+AM^2}}=\dfrac{5\sqrt{3}}{3}\)
c.
Do \(AD\perp\left(ABC\right)\) theo cmt \(\Rightarrow AM\) là hình chiếu vuông góc của DM lên (ABC)
\(\Rightarrow\widehat{DMA}\) là góc giữa DM và (ABC)
\(tan\widehat{DMA}=\dfrac{AD}{AM}=\sqrt{2}\Rightarrow\widehat{DMA}\approx54^044'\)

Góc giữa AC với mặt phẳng (ABD) là góc KAC vì CK ⊥ (ABD) nên AK là hình chiếu của AC trên mặt phẳng (ABD).
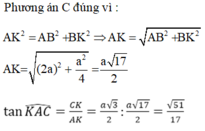
Đáp án C

a: BH vuông góc SA
BH vuông góc AC
=>BH vuông góc (SAC)
b: (SC;ABCD)=(CS;CA)=góc SCA
\(AC=\sqrt{a^2+\left(\dfrac{1}{5}a\right)^2}=\dfrac{a\sqrt{26}}{5}\)
\(SC=\sqrt{SA^2+AC^2}=\dfrac{3\sqrt{14}}{5}\)a
\(sinSCA=\dfrac{SA}{SC}=\dfrac{2a}{\dfrac{3\sqrt{14}}{5}a}=\dfrac{5\sqrt{14}}{21}\)
=>góc SCA=63 độ

(Vẽ hình: A là đỉnh của tứ diện, BCD là đáy của tứ diện)
+ Trên mặt phẳng đáy BCD kẻ các đường cao của tam giác BCD là BE, CF, DK.Ba đường cao gặp nhau tại H.
+ Xét mặt phẳng ABE
CD vuông góc BE
CD vuông góc AB
=> CD vuông góc với mặt phẳng ABE => CD vuông góc với AH (1)
+ Xét mặt phẳng ACF
BD vuông góc AC
BD vuông góc CF
=> BD vuông góc với mặt phẳng ACF => BD vuông góc với AH (2)
+ Từ (1) và (2) => AH vuông góc BCD
=> AH vuông góc với BC
Mà BC vuông góc với DK
=> BC vuông góc với mp ADK => BC vuông góc với AD
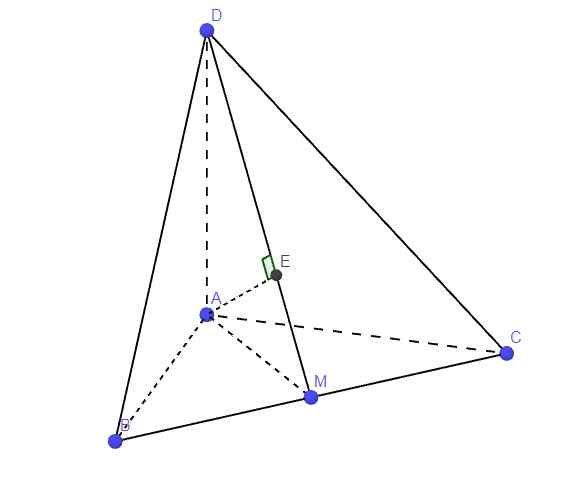

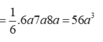
AB vuông góc BC
AB vuông góc BD
=>AB vuông góc (BCD)
=>AB vuông góc CD
BC vuông góc CD
AB vuông góc CD
=>CD vuông góc (BCA)
=>CD vuông góc BH
=>(BH;CD)=90 độ