Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi H là hình chiếu vuông góc của A lên (BCD)
\(AB=AC=AD\Rightarrow HA=HB=HC\Rightarrow H\) là tâm đáy
\(\Rightarrow DH\perp BC\)
Mà \(AH\perp\left(BCD\right)\Rightarrow AH\perp BC\)
\(\Rightarrow BC\perp\left(ADH\right)\Rightarrow BC\perp AD\)
b/ Chắc bạn nhầm đề?
Hoàn toàn tương tự câu a, ta chứng minh được \(CD\perp\left(ABH\right)\Rightarrow CD\perp AB\Rightarrow\left(AB;CD\right)=90^0\)
Điểm I để làm gì nhỉ? :<

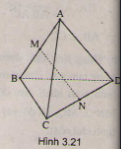
A B C D M N P Q
a/ Trong mp (BCD) dựng đường thẳng // với CD cắt BD tại P => CD//NP (1)
=> mp (MNP) là mp \(\alpha\)
Trong mp (ACD) từ M dựng đường thẳng //CD cắt AC tại Q => CD//MQ (2)
Từ (1) và (2) => NP//MQ => MPNQ là thiết diện của tứ diện ABCD với mp \(\alpha\)
b/
Xét tg ACD có
MQ//CD và MA=MD => QA=QC (trong tam giác đường thẳng đi qua trung điểm của 1 cạnh và // với 1 cạnh thì đi qua trung điểm cạnh còn lại của tam giác => MQ là đường trung bình của tg ACD \(\Rightarrow MQ=\frac{CD}{2}\)
Ta có MQ//NP để MPNQ là hình bình hành thì \(MQ=NP=\frac{CD}{2}\) (tứ giác có 1 cặp cạnh đối // và = nhau thì tứ giác là hbh)
=> NP là đường trung bình của tg BCD => N là trung điểm của BC


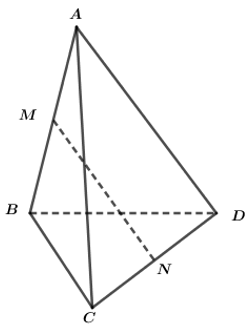


Đáp án A
Ta có: