Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách làm của bạn trên sai rồi nhưng đáp số đúng làm lại cho tự vẽ hình lấy :))
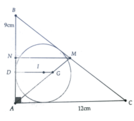
Gọi D là tiếp điểm của đường tròn (I) với AB. Ta tính được BC = 15 ( cm )
\(AD=\frac{AB+AC-BC}{2}=\frac{9+12-15}{2}=3\left(cm\right)\)
Gọi N là giao điểm của BI và AC. Ta có:
\(\frac{BI}{BN}=\frac{BD}{BA}=\frac{6}{9}=\frac{2}{3}=\frac{BM}{BG}\Rightarrow\)IG // NM và \(IG=\frac{2}{3}NM\)
Lần lượt tính AN = 4,5 ( cm ) ; AM = 6 ( cm )
Suy ra NM = 1,5 ( cm ) nên IG = 1( cm )
Vậy IG = 1 ( cm )
Gọi J,D thứ tự là trung điểm BC,BA.
Hạ: GE', IE  BA.
BA.
JD là đường trung bình  ABC nên: JD = 1/2AC = 6
ABC nên: JD = 1/2AC = 6
JA = 1/2BC = 15/2
AD = 1/2AB = 9/2
AG/AJ = AE'/AD = 2/3 => AE' = 3
Lại có: AE = AC + AB - BC/2 = 3 => E \(\equiv\) E' => G; I; E
=> IG = EG' - IE' = 1 (cm)
*P/s: Sai đâu thì bn sửa nhé*

Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm


a) Gọi D, E, F lần lượt là chân các đường phân giác của tam giác ABC lần lượt hạ từ A, B, C.
Gọi T là trung điểm của BC. Do AD là đường phân giác của tam giác ABC nên \(\frac{BD}{AB}=\frac{CD}{AC}\Rightarrow\frac{BD}{5}=\frac{CD}{7}=\frac{BD+CD}{5+7}=\frac{6}{12}=\frac{1}{2}\)\(\Rightarrow\hept{\begin{cases}BD=2,5\\CD=3,5\end{cases}}\)
\(\Delta ABD\) có BI là đường phân giác nên \(\frac{AI}{ID}=\frac{BA}{BD}=\frac{5}{2,5}=2\)
Do G là trọng tâm của tam giác ABC nên \(\frac{AG}{GT}=2\)
Từ các kết quả trên ta được \(\frac{AI}{ID}=\frac{AG}{GT}=2\)suy ra IG // DT hay IG // BC (Theo định lý Thales đảo)
b) Ta có \(\Delta BMI=\Delta BDI\)vì \(BD=BM=2,5;\widehat{DBI}=\widehat{MBI}\); BI là cạnh chung
Suy ra \(\widehat{BMI}=\widehat{BDI}\)
Chứng minh tương tự \(\Delta CNI=\Delta CDI\Rightarrow\widehat{ CNI}=\widehat{CDI}\)
Mà \(\widehat{BDI}+\widehat{CDI}=180^0\)nên \(\widehat{BMI}+\widehat{CNI}=180^0\)suy ra\(\widehat{AMI}+\widehat{ANI}=180^0\)
Vậy tứ giác AMIN nội tiếp hay bốn điểm A, M, I, N cùng nằm trên 1 đường tròn (đpcm)

nếu rảnh có thể tham khảo tại
Trường Toán Pitago – Hướng dẫn Giải toán - Học toán lớp 3,4,5,6,7,8,9 - Học toán trên mạng - Học toán online

a. Ta thấy ˆHDC=ˆHEC=90oHDC^=HEC^=90o nên CDHE là tứ giác nội tiếp đường tròn đường kính HC.
b. Ta thấy ngay ˆIAC=ˆKBCIAC^=KBC^ (Cùng phụ với góc ACB) nên \wideba=\widebatKC\wideba=\widebatKC (Góc nội tiếp)
suy ra IC = KC ( Liên hệ giữa cung và dây)
Vậy nên tam giác IKC cân tại C.
c. Do \wideba=\widebatKC\wideba=\widebatKC nên ˆKAC=ˆACIKAC^=ACI^ (Góc nội tiếp)
Xét tam giác AHK có AE vừa là đường cao, vừa là phân giác nên AHK là tam giác cân tại A, hay AH = AK.
d. Ta thấy do BOF là đường kính nên ˆBCF=90o⇒BCF^=90o⇒ AH // FC (Cùng vuông góc với BC).
Tương tự AF // HC vì cùng vuông góc với AB. Vậy thì AFCH là hình bình hành hay AC giao FH tại trung điểm mỗi đường.
P là trung điểm AC nên F cũng là trung điểm FH. Vậy F, H, P thẳng hàng.
