Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

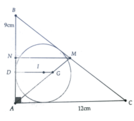
Gọi M là trung điểm của BC
Ta tính được AG = 2 3 AM = 10cm
Gọi N là trung điểm của AB => MN//AC, MN ⊥ AB
D,I,G thẳng hàng
<=> A G A M = A D A N = 2 3 <=> A D 2 A N = 1 3 <=> A D A B = 1 3
Ta có AD = r nội tiếp = A B + A C - B C 2 <=> A B 3 = A B + A C - B C 2
<=> AB+3AC = 3BC = A B 2 + A C 2
<=> 3AC = 4AB (đpcm)
Áp dụng kết quả trên ta có: AD = A B + A C - B C 2 = 3cm
=> ID = DA = 3cm => IG = DG – ID = 1cm

Cách làm của bạn trên sai rồi nhưng đáp số đúng làm lại cho tự vẽ hình lấy :))
Gọi D là tiếp điểm của đường tròn (I) với AB. Ta tính được BC = 15 ( cm )
\(AD=\frac{AB+AC-BC}{2}=\frac{9+12-15}{2}=3\left(cm\right)\)
Gọi N là giao điểm của BI và AC. Ta có:
\(\frac{BI}{BN}=\frac{BD}{BA}=\frac{6}{9}=\frac{2}{3}=\frac{BM}{BG}\Rightarrow\)IG // NM và \(IG=\frac{2}{3}NM\)
Lần lượt tính AN = 4,5 ( cm ) ; AM = 6 ( cm )
Suy ra NM = 1,5 ( cm ) nên IG = 1( cm )
Vậy IG = 1 ( cm )
Gọi J,D thứ tự là trung điểm BC,BA.
Hạ: GE', IE  BA.
BA.
JD là đường trung bình  ABC nên: JD = 1/2AC = 6
ABC nên: JD = 1/2AC = 6
JA = 1/2BC = 15/2
AD = 1/2AB = 9/2
AG/AJ = AE'/AD = 2/3 => AE' = 3
Lại có: AE = AC + AB - BC/2 = 3 => E \(\equiv\) E' => G; I; E
=> IG = EG' - IE' = 1 (cm)
*P/s: Sai đâu thì bn sửa nhé*

Lấy G là trọng tâm của ΔABC
⇒CG=2/3CD
Vẽ đường cao AH của ΔABC , vì ΔABC cân tại A ⇒AH vừa là đường cao vừa là trung tuyến
⇒ A,G,H thẳng hàng.(1)
OB=OC=R ⇒ O thuộc đường trung trực của BC
⇒A,O,H thẳng hàng (2)
Từ (1) và(2) ⇒ OG vuông góc với BC
Lấy M là trung điểm của AC. ΔABC có D,M lần lượt là trung điểm của AB,AC
⇒DM//BC
Mà OGvuông góc với BC
⇒OG vuông góc với DM
⇒OG vuông góc với DE (3)
ΔAOB có OA=OB
⇒ΔAOB cân tại O mà D là trung điểm của AB
⇒OD vuông góc với AB
Gọi N là trung điểm của AD. Vì E là trọng tâm của ΔACD
⇒CE=2/3CN
ΔCND có CE=2/3CN,CG=2/3CD
⇒GE//DN ( theo định lý Ta lét)
⇒GE//AB mà OD vuông góc với AB
⇒OD vuông góc với GE (4)
Từ (3),(4) ⇒ΔDGE có OD vuông góc với GE, OG vuông góc DE
⇒O là trực tâm của ΔDGE
⇒OE vuông góc với DG hay OE vuông góc với CD
Lấy G là trọng tâm của ΔABC
⇒CG=23CD
Vẽ đường cao AH của ΔABC , vì ΔABC cân tại A ⇒AH vừa là đường cao vừa là trung tuyến
⇒ A,G,H thẳng hàng.(1)
OB=OC=R ⇒ O thuộc đường trung trực của BC
⇒A,O,H thẳng hàng (2)
Từ (1) và(2) ⇒ OG vuông góc với BC
Lấy M là trung điểm của AC. ΔABC có D,M lần lượt là trung điểm của AB,AC
⇒DM//BC
Mà OGvuông góc với BC
⇒OG vuông góc với DM
⇒OG vuông góc với DE (3)
ΔAOB có OA=OB
⇒ΔAOB cân tại O mà D là trung điểm của AB
⇒OD vuông góc với AB
Gọi N là trung điểm của AD. Vì E là trọng tâm của ΔACD
⇒CE=23CN
ΔCND có CE=23CN,CG=23CD
⇒GE//DN ( theo định lý Ta lét)
⇒GE//AB mà OD vuông góc với AB
⇒OD vuông góc với GE (4)
Từ (3),(4) ⇒ΔDGE có OD vuông góc với GE, OG vuông góc DE
⇒O là trực tâm của ΔDGE
⇒OE vuông góc với DG hay OE vuông góc với CD
krfykof67777777777777777777777777777777
???????????????????/