Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, tứ giác EHFA có : góc A= góc E = góc F =90 độ ( GT )
=>> EHFA là HCN
=>> AH = EF ( hai đường chéo HCN )
b, mình hơi vội nên mình gợi ý cho bạn câu b thế này ạ ! CM tam giác BAC ~ tam giác EAF
=>> AE/AF=AC/AB
=>> AE.AB=AF.AC
kẻ hộ mình cái hình
a)Xét tứ giác AEHF có góc A=góc E = góc F= 90 độ nên AEHF là hình chữ nhật
Do đó AH=EF theo tính chất 2 đường chéo của hcn
b)chưa có hình chưa làm được

a) tam giác ABC vuông tại A nên áp dụng Py-ta-go
\(\Rightarrow AB^2=BC^2-AC^2=15^2-12^2=81\Rightarrow AB=9\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH.BC=AB.AC\Rightarrow AH=\dfrac{AB.AC}{BC}=\dfrac{12.9}{15}=\dfrac{36}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AB^2=BH.BC\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{9^2}{15}=\dfrac{27}{5}\left(cm\right)\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AC^2=CH.BC\Rightarrow CH=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=\dfrac{48}{5}\left(cm\right)\)
b) tam giác AHB vuông tại H có đường cao HE nên áp dụng hệ thức lượng
\(\Rightarrow AE.AB=AH^2\)
tam giác AHC vuông tại HA có đường cao HF nên áp dụng hệ thức lượng
\(\Rightarrow AF.AC=AH^2=AE.AB\)
c) Vì \(\angle HEA=\angle HFA=\angle EAF=90\Rightarrow AEHF\) là hình chữ nhật
\(\Rightarrow AH=EF\)
tam giác EHF vuông tại H nên áp dụng Py-ta-go
\(\Rightarrow HE^2+HF^2=EF^2=AH^2\)
tam giác ABC vuông tại A có đường cao AH nên áp dụng hệ thức lượng
\(\Rightarrow AH^2=HB.HC\Rightarrow HE^2+HF^2=HB.HC\)

Câu b: Xet tg vuông AEH và tg vuông ABC có
^BAH = ^ACB (cùng phụ với ^ABC)
=> Tg AEH đồng dạng với tg ABC \(\Rightarrow\frac{AE}{AC}=\frac{EH}{AB}\) mà EH=AF (cạnh đối HCN)
\(\Rightarrow\frac{AE}{AC}=\frac{AF}{AB}\Rightarrow AE.AB=AF.AC\)
Câu c:
Ta có AM=BC/2==BM=CM (trong tg vuông trung tuyến thuộc cạnh huyền bằng nửa cạnh huyền)
=> tg AMC cân tại M => ^MAC = ^ACB mà ^BAH = ^ACB (cmt) => ^MAC = ^BAH (1)
Ta có ^AHE = ^ABC (cùng phụ với ^BAH) mà ^AHE = ^HAC (góc so le trong) => ^ABC = ^HAC (2)
Gọi giao của AH với EF là O xét tg AOF có
AH=EF (hai đường chéo HCN = nhau)
O là trung điểm của AH vào EF
=> OA=OF => tg AOF cân tại O => ^HAC = ^AFE (3)
Từ (2) và (3) => ^AFE = ^ABC (4)
Mà ^ABC + ^ACB = 90 (5)
Từ (1) (4) (5) => ^MAC + ^AFE = 90
Xét tg AKF có ^AKF = 180 - (^MAC + ^AFE) = 180-90=90 => AM vuông góc EF tại K

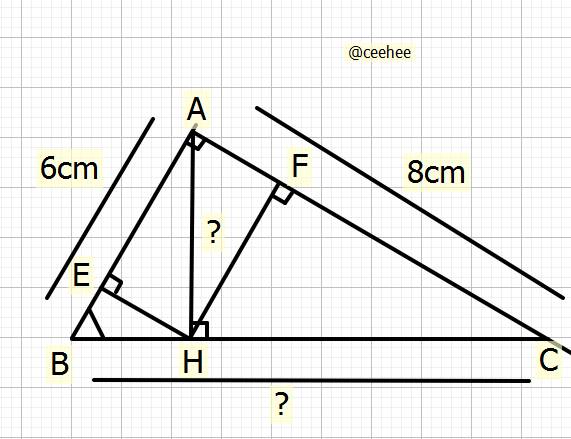
`a)` Tỉ số lượng giác góc `B` của \(\Delta ABC\)
\(SinB=\dfrac{AC}{BC}\\ CosB=\dfrac{AB}{BC}\\ TanB=\dfrac{AC}{AB}\\ CotB=\dfrac{AB}{AC}\)
`b)` Tính `BC,AH`
Xét \(\Delta ABC\) vuông tại `A`, đường cao `AH`
Ta có: \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\left(htl\right)\)
\(\Rightarrow\dfrac{1}{AH^2}=\dfrac{1}{6^2}+\dfrac{1}{8^2}\\ \Rightarrow\dfrac{1}{AH^2}=\dfrac{25}{576}\\ \Rightarrow AH^2=\dfrac{576\cdot1}{25}=23,04\\ \Rightarrow AH=\sqrt{23,04}=4,8cm\)
Ta có: \(AB\cdot AC=AH\cdot BC\left(htl\right)\)
\(\Rightarrow6\cdot8=4,8\cdot BC\\ \Rightarrow48=4,8\cdot BC\\ \Rightarrow BC=\dfrac{48}{4,8}\\ \Rightarrow BC=10cm\)
Vậy: `AH = 4,8cm; BC= 10cm`
`c)` C/m: `AE * AB = AF * AC`
Xét \(\Delta AHB\) vuông tại `H`, đường cao `HE`
Ta có: \(AH^2=AE\cdot AB\left(htl\right)\) `(1)`
Xét \(\Delta AHC\) vuông tại `H`, đường cao `HF`
Ta có: \(AH^2=AF\cdot AC\left(htl\right)\) `(2)`
Từ `(1)` và `(2)` \(\Rightarrow AH^2=AH^2\)
\(\Rightarrow AE\cdot AB=AF\cdot AC\left(=AH^2\right).\)

Hệ thức lượng: \(AH^2=BH.CH\)
Hai tam giác vuông BEH và HFC đồng dạng: \(\Rightarrow\dfrac{BE}{FH}=\dfrac{EH}{CF}\Rightarrow BE.CF=EH.FH\)
Hai tam giác vuông AEH và CFH đồng dạng \(\Rightarrow\dfrac{AH}{CH}=\dfrac{EH}{FH}\Rightarrow AH.FH-CH.EH=0\)
Hai tam giác vuông BEH và AFH đồng dạng \(\Rightarrow\dfrac{BH}{AH}=\dfrac{EH}{FH}\Rightarrow EH.AH-BH.FH=0\)
Ta có: \(\left(BE\sqrt{CH}+CF\sqrt{BH}\right)^2=BE^2.CH+CF^2.BH+2BE.CF.\sqrt{BH.CH}\)
\(=BE^2.CH+CF^2.BH+2BE.CF.AH\)
\(=\left(BH^2-EH^2\right)CH+\left(CH^2-FH^2\right)BH+2BE.CF.AH\)
\(=BH.CH\left(BH+CH\right)-EH^2.CH-FH^2.BH+2EH.FH.AH\)
\(=AH^2.BC+EH\left(AH.FH-EH.CH\right)+FH\left(AH.EH-FH.BH\right)\)
\(=AH^2.BC=\left(AH\sqrt{BC}\right)^2\)
\(\Rightarrow BE\sqrt{CH}+CF\sqrt{BH}=AH\sqrt{BC}\)

1: AH=căn 4*9=6cm
AB=căn 4*13=2căn 13(cm)
AC=căn 9*13=3*căn 13(cm)
2: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>DE=AH
=>DE^2=HB*HC
3: ΔAHB vuông tại H có HD vuông góc AB
nên AD*AB=AH^2
ΔAHC vuông tại H có HE vuông góc AC
nên AE*AC=AH^2
=>AD*AB=AE*AC
4: BD*BA+AE*AC
=AH^2+BH^2=AB^2
5: AD*AB=AE*AC
=>AD/AC=AE/AB
=>ΔADE đồng dạng với ΔACB
6: góc AED+góc MAC
=góc AHD+góc MCA
=góc ABC+góc ACB=90 độ
=>DE vuông góc AM
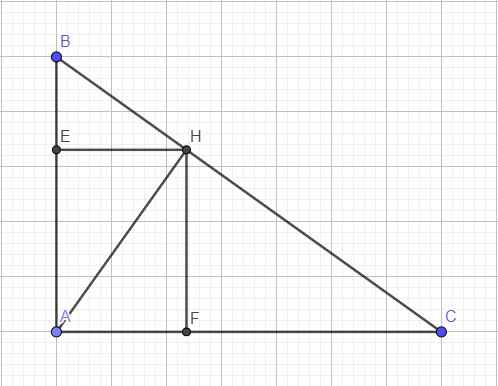
b) Xét tam giác ABH vuông tại H có HE là đường cao
⇒ AE.AB = AH2 (1)
Xét tam giác AHC vuông tại H có HF là đường cao
⇒ AF.AC = A H 2 (2)
Từ (1) và (2) ⇒ AE.AB = AF.AC