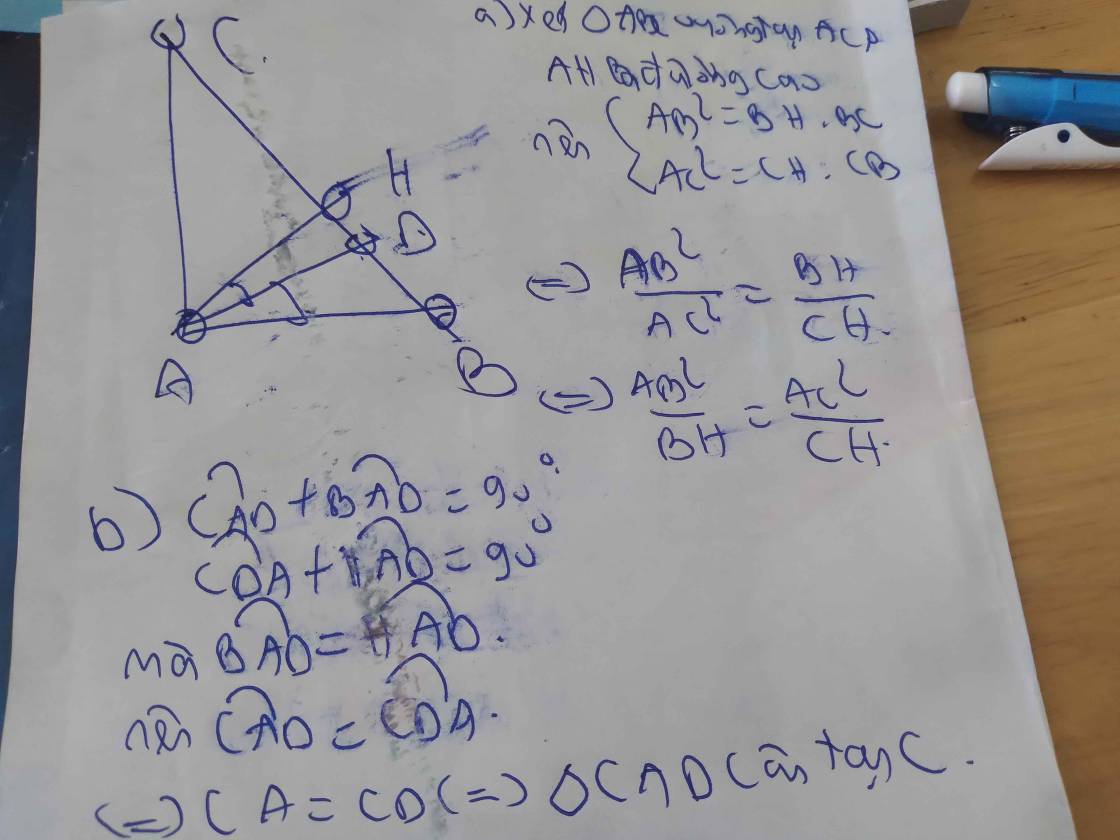Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn tk câu này mình làm rồi:
Cho ΔABC nhọn, đường cao AH. Gọi D, E lần lượt là hình chiếu của H trên AB, AC.CMR:a) DE=AH.SinAb) Cho AI là phân giác g... - Hoc24
nhớ đổi điểm I thành điểm D

Kẻ \(AH\perp BC\) tại H
Áp dụng hệ thức lượng trong tam giác vuông BAC có:
\(\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AH^2}\)
Do AD và AE lần lượt là hai tia phân giác trong và ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\)
Áp dụng hệ thức lượng vào tam giác vuông AED có:
\(\dfrac{1}{AE^2}+\dfrac{1}{AD^2}=\dfrac{1}{AH^2}\) (AH là đường cao của tam giác AED do \(AH\perp BC\) hay \(AH\perp ED\))
\(\Rightarrow\dfrac{1}{AB^2}+\dfrac{1}{AC^2}=\dfrac{1}{AE^2}+\dfrac{1}{DA^2}\)
Vậy...

a: Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC và AC^2=CH*BC
=>AB^2/AC^2=BH/CH
b: S AHC=8,64
=>1/2*AH*HC=8,64
=>AH*HC=17,28
S AHB=15,36
=>1/2*AH*HB=15,36
=>AH*HB=30,72
mà AH*HC=17,28
nên AH*AH*HB*HC=30,72*17,28
=>AH^2*AH^2=30,72*17,28
=>AH^4=530,8416
=>\(AH=\sqrt[4]{530.8416}=4.8\left(cm\right)\)

1: Xét ΔABC vuông tại A có
\(BC^2=AB^2+AC^2\)
hay BC=5(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
hay AH=2,4(cm)

a)
Kẻ DH _I_ AB và DK _I_ AC.
\(\widehat{DHA}=\widehat{HAK}=\widehat{AKD}=90^0\)
=> AKDH là hình chữ nhật có AD là đường phân giác
=> AKDH là hình vuông
=> AK = KD = DH = HA
Tam giác KAD vuông cân tại A có:
\(AD=\sqrt{2}AK\)
\(\Rightarrow\dfrac{\sqrt{2}}{AD}=\dfrac{1}{AK}\left(1\right)\)
~*~*~*~*~
\(S_{DAB}+S_{DAC}=S_{ABC}\)
\(\Leftrightarrow\dfrac{1}{2}DH\times AB+\dfrac{1}{2}KD\times AC=\dfrac{1}{2}AB\times AC\)
\(\Leftrightarrow AK\times\left(AB+AC\right)=AB\times AC\)
\(\Leftrightarrow\dfrac{AB+AC}{AB\times AC}=\dfrac{1}{AK}\)
\(\Leftrightarrow\dfrac{1}{AB}+\dfrac{1}{AC}=\dfrac{1}{AK}\left(2\right)\)
~*~*~*~*~
(1) và (2) => đpcm
b)
Trên đoạn thẳng AB, lấy điểm E sao cho AD = AE.
AD là đường phân giác của tam giác ABC
\(\Rightarrow\widehat{DAB}=\widehat{DAC}=\dfrac{\widehat{BAC}}{2}=\dfrac{120^0}{2}=60^0\)
Tam giác ABC có AD là đường phân giác
=> \(\dfrac{BD}{AB}=\dfrac{DC}{AC}=\dfrac{BD+DC}{AB+AC}=\dfrac{BC}{AB+AC}\) (tính chất của dãy tỉ số bằng nhau)
=> \(\dfrac{BD}{BC}=\dfrac{AB}{AB+AC}\)
Tam giác ADE có: AD = AE, \(\widehat{DAE}=60^0\)
=> Tam giác ADE đều
=> \(\widehat{EDA}=\widehat{DAC}\left(=60^0\right)\) mà chúng nằm ở vị trí so le trong
=> ED // AC
\(\Rightarrow\dfrac{ED}{AC}=\dfrac{BD}{BC}=\dfrac{AB}{AB+AC}\)
\(\Rightarrow\dfrac{1}{AD}=\dfrac{AB+AC}{AB\times AC}=\dfrac{1}{AB}+\dfrac{1}{AC}\left(\text{đ}pcm\right)\left(ED=AD\right)\)