Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Delta'\) = (-m2)2 - m2 - 2 = m4 - m2 - 2
để pt có 2 nghiệm x1, x2 thì m4 - m2 - 2 \(\ge\) 0
=> (m2 - \(\dfrac{1}{2}\))2 - \(\dfrac{9}{4}\) \(\ge\) 0
\(\left\{{}\begin{matrix}m^2-\dfrac{1}{2}\le-\dfrac{3}{2}\\m^2-\dfrac{1}{2}\ge\dfrac{3}{2}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}m^2\le-1\left(loai\right)\\m^2\ge2\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}m\ge\sqrt{2}\\m\le-\sqrt{2}\end{matrix}\right.\)
theo hệ thức Vi - ét : \(\left\{{}\begin{matrix}x_1+x_2=2m^2\\x_1.x_2=m^2+2\end{matrix}\right.\)
ta có : \(\dfrac{1}{\sqrt{2}}\)x1x2 = 3\(\sqrt{x_1+x_2}\) <=> \(\dfrac{1}{\sqrt{2}}\).(m2 + 2) - 3.\(\sqrt{2m^2}\) = 0
<=> \(\dfrac{\sqrt{2}.m^2}{2}\) + \(\sqrt{2}\) - \(3\sqrt{2}.m\) = 0
<=> m2 - 6m + 2 = 0
\(\Delta'\) = (-3)2 - 2 = 7 > 0 => pt có 2 nghiệm pb
m1 = \(\dfrac{3-\sqrt{7}}{1}\) = 3-\(\sqrt{7}\) ( loại )
m2 = 3+\(\sqrt{7}\) (TM )
vậy để pt có 2 nghiêm jthoar mãn đk trên thì m = 3+\(\sqrt{7}\)

\(x^2-4mx+m^2-2m+1=0\)
\(\Delta'=\left(-2m\right)^2-\left(m^2-2m+1\right)=4m^2-m^2+2m-1=3m^2+2m-1\)
* Pt có 2 nghiệm phân biệt \(\Leftrightarrow\Delta'>0\Leftrightarrow3m^2+2m-1>0\Leftrightarrow\left[{}\begin{matrix}m< -1\\m>\frac{1}{3}\end{matrix}\right.\)
* Ta có: \(a.c=m^2-2m+1=\left(m-1\right)^2\ge0\)
=> x1, x2 không thể có hai nghiệm trái dấu
* Pt có 2 nghiệm phân biệt khi \(\left[{}\begin{matrix}m< -1\\m>\frac{1}{3}\end{matrix}\right.\) (1)
Theo định lí Vi-ét: \(\left\{{}\begin{matrix}S=x_1+x_2=4m\\P=x_1x_2=\left(m-1\right)^2\end{matrix}\right.\)
\(\left|\sqrt{x_1}-\sqrt{x_2}\right|=1\)
\(\Rightarrow\left(\sqrt{x_1}-\sqrt{x_2}\right)^2=1\)
\(\Leftrightarrow x_1-2\sqrt{x_1x_2}+x_2=1\)
\(\Leftrightarrow x_1+x_2-2\sqrt{x_1x_2}=1\)
\(\Leftrightarrow4m-2\sqrt{\left(m-1\right)^2}=1\)
\(\Leftrightarrow-2\left|m-1\right|=1-4m\)
\(\Leftrightarrow\left|m-1\right|=2m-\frac{1}{2}\)
ĐK: \(2m-\frac{1}{2}\ge0\Leftrightarrow m\ge\frac{1}{4}\)
+ TH1: \(m-1=2m-\frac{1}{2}\Leftrightarrow m=-\frac{1}{2}\) (0 t/m)
+ TH2: \(m-1=\frac{1}{2}-2m\Leftrightarrow3m=\frac{3}{2}\Leftrightarrow m=\frac{1}{2}\) (t/m) (2)
(1),(2): Vậy \(m=\frac{1}{2}\) thỏa mãn đề bài

\(\Delta'=1-\left(2m-1\right)=2-2m\ge0\Rightarrow m\le1\)
Để biểu thức đề bài xác định thì pt có 2 nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2>0\\x_1x_2=2m-1>0\end{matrix}\right.\) \(\Rightarrow m>\frac{1}{2}\)
\(\frac{1}{\sqrt{x_1}}+\frac{1}{\sqrt{x_2}}=2\Leftrightarrow\sqrt{x_1}+\sqrt{x_2}=2\sqrt{x_1x_2}\)
\(\Leftrightarrow x_1+x_2+2\sqrt{x_1x_2}=4x_1x_2\)
\(\Leftrightarrow2+2\sqrt{2m-1}=4\left(2m-1\right)\)
\(\Leftrightarrow2\left(2m-1\right)-\sqrt{2m-1}-1=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{2m-1}=1\\\sqrt{2m-1}=-\frac{1}{2}\left(l\right)\end{matrix}\right.\) \(\Rightarrow m=1\) (thỏa mãn)

Ta có: \(a-b+c=1+2m-2m-1=0\)
Phương trình luôn có 2 nghiệm: \(\left\{{}\begin{matrix}x_1=-1\\x_2=2m+1\end{matrix}\right.\)
Để biểu thức bài toán xác định thì:
\(\left\{{}\begin{matrix}x_1+x_2=2m\ge0\\3+x_1x_2=2-2m\ge0\end{matrix}\right.\) \(\Rightarrow0\le m\le1\)
\(\sqrt{x_1+x_2}+\sqrt{3+x_1x_2}=2m+1\)
\(\Leftrightarrow\sqrt{2m}+\sqrt{2-2m}=2m+1\)
\(\Leftrightarrow2m-\sqrt{2m}+1-\sqrt{2-2m}=0\)
\(\Leftrightarrow\frac{4m^2-2m}{2m+\sqrt{2m}}+\frac{2m-1}{1+\sqrt{2-2m}}=0\)
\(\Leftrightarrow\left(2m-1\right)\left(\frac{2m}{2m+\sqrt{2m}}+\frac{1}{1+\sqrt{2-2m}}\right)=0\)
\(\Leftrightarrow2m-1=0\Rightarrow m=\frac{1}{2}\)

b) Để phương trình có nghiệm thì \(\Delta'=\left(-m\right)^2-\left(m-1\right)\ge0\Leftrightarrow m^2-m+1\ge0\)
Điều này hiển nhiên vì \(m^2-m+1=\left(m-\frac{1}{2}\right)^2+\frac{3}{4}>0\forall m\)
Theo đề bài suy ra \(x_1+x_2+2\sqrt{x_1x_2}=4\) (bình phương hai vế của giả thiết)
Chị thay tiếp vô hệ thức Viet và em không chắc.
Xét \(\Delta^,=\left(-m\right)^2-\left(m-1\right)\)\(=m^2-m+1\)
\(=(m^2-2\cdot m\cdot\frac{1}{2}+\frac{1}{4})+\frac{3}{4}\)\(=\left(m-\frac{1}{2}\right)^2+\frac{3}{4}>0\)với mọi m
Theo Vi- ét :\(\hept{\begin{cases}x_1+x_2=2m\\x_1\cdot x_2=m-1\end{cases}}\)(1)
Theo bài ra ta có : \(\sqrt{x_1}+\sqrt{x_2}=2\)
\(\Leftrightarrow\left(\sqrt{x_1}+\sqrt{x_2}\right)^2=4\)\(\Leftrightarrow x_1+2\sqrt{x_1\cdot x_2}+x_2=4\)
\(\Leftrightarrow\left(x_1+x_2\right)+2\sqrt{x_1\cdot x_2}=4\)(*)
Thay (1) vào (*) ta được :
\(2m+2\sqrt{m-1}=4\)\(\Leftrightarrow2\sqrt{m-1}=4-2m\)
\(\Leftrightarrow\sqrt{m-1}=2-m\)\(\Leftrightarrow\sqrt{m-1}^2=\left(2-m\right)^2\)
\(\Leftrightarrow|m-1|=4-4m+m^2\)
\(\Leftrightarrow\orbr{\begin{cases}m-1=4-4m+m^2\\m-1=-4+4m-m^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}m^2-5m+5=0\left(2\right)\\m^2-3m+3=0\left(3\right)\end{cases}}\)
\(\Delta_{\left(2\right)}=\left(-5\right)^2-4\cdot5=5>0\)
=> Phương trình có 2 nghiệm phân biệt
\(m_1=\frac{5+\sqrt{5}}{2};m_2=\frac{5-\sqrt{5}}{2}\)
\(\Delta_{\left(3\right)}=\left(-3\right)^2-4\cdot3=-3< 0\)
=> phương trình vô nghiệm
KL : ....
kb vs mk nha

\(x^2-4x+2m-3=0\)
\(\Delta=\left(-4\right)^2-4\left(2m-3\right)=16-8m+12=28-8m\)
Để pt có hai nghiệm x1, x2 thì \(\Delta\ge0\)
<=> \(28-8m\ge0\) <=> \(m\le\frac{7}{2}\)
Áp dụng ht viet có: \(\left\{{}\begin{matrix}x_1+x_2=4\\x_1.x_2=2m-3\end{matrix}\right.\)
Có: \(\sqrt{x_1^2}+\sqrt{x_2^2}=4\)
<=> \(x_1^2+x^2_2+2\sqrt{x^2_1.x^2_2}=16\)
<=> \(\left(x_1+x_2\right)^2-2x_1x_2+2\sqrt{\left(2m-3\right)^2}=16\)
<=>\(4^2-2\left(2m-3\right)\left|2m-3\right|=16\)
<=> \(\left(2m-3\right)\left|2m-3\right|=0\)
=>\(\left[{}\begin{matrix}2m-3=0\\\left|2m-3\right|=0\end{matrix}\right.\) =>\(m=\frac{3}{2}\)(t/m)
Vậy \(m=\frac{3}{2}\).
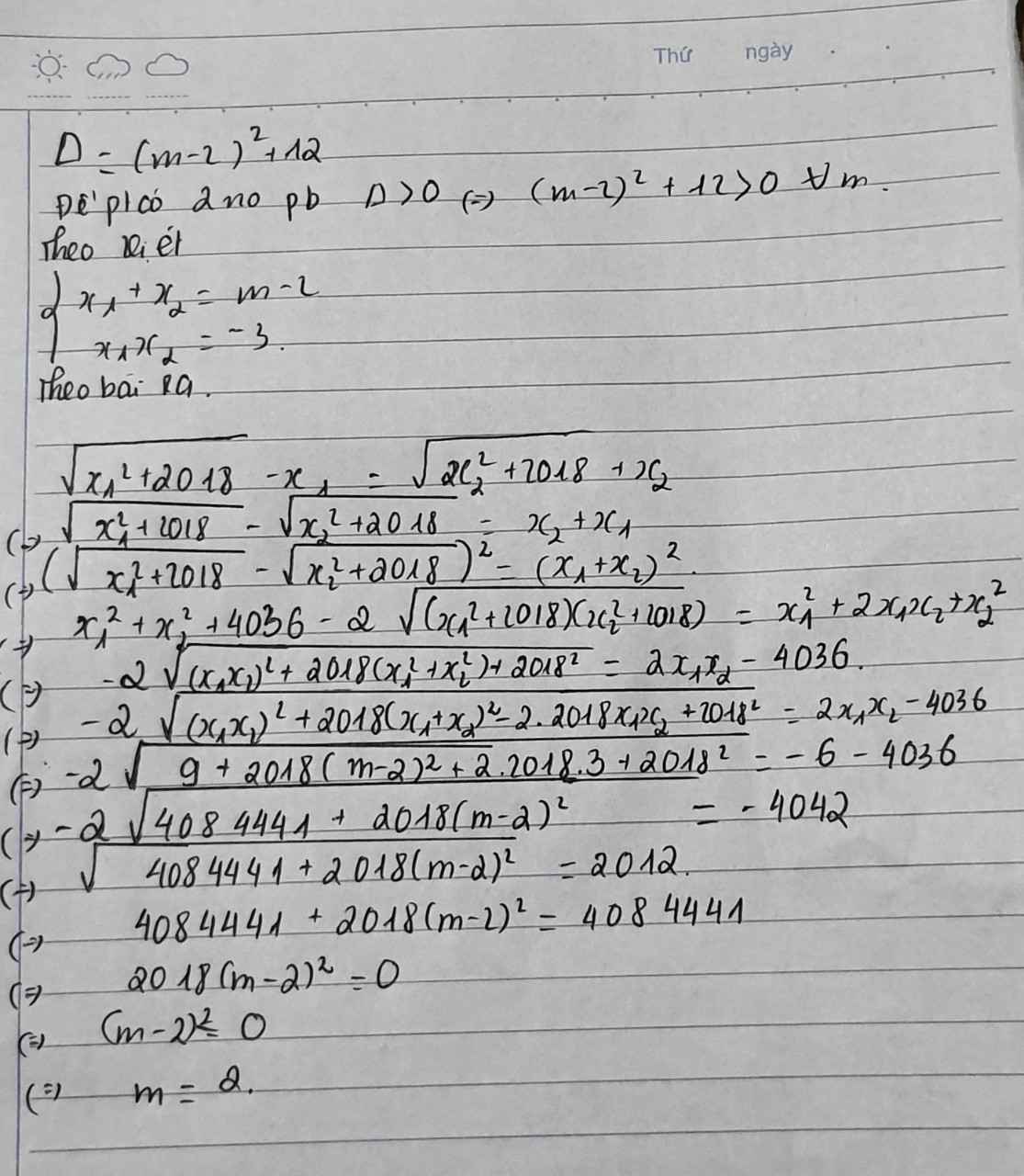
\(\text{Δ}=\left(m+3\right)^2-4m^2\)
\(=m^2+6m+9-4m^2=-3m^2+6m+9\)
\(=-3\left(m^2-2m-3\right)=-3\left(m-3\right)\left(m+1\right)\)
Để phương trình có hai nghiệm phân biệt thì (m-3)(m+1)<0
=>-1<m<3
b:\(\Leftrightarrow x1+x2+2\sqrt{x_1x_2}=5\)
\(\Leftrightarrow m+3+2\sqrt{m^2}=5\)
=>2|m|=5-m-3=2-m
TH1: m>=0
=>2m=2-m
=>3m=2
=>m=2/3(nhận)
TH2: m<0
=>-2m=2-m
=>-2m+m=2
=>m=-2(loại)
c: P(x1)=P(x2)
=>\(x_1^3+a\cdot x_1^2+b=x_2^3+a\cdot x_2^2+b\)
=>\(\left(x_1-x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)+a\left(x_1-x_2\right)\left(x_1+x_2\right)=0\)
=>(x1-x2)(x1^2+x1x2+x2^2+ax1+ax2)=0
=>x=0 và a=0
=>\(\left\{{}\begin{matrix}a=0\\b\in R\end{matrix}\right.\)