Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: \(PT\Leftrightarrow x^2+\left(m-3\right)x-m=0\)
\(\text{Δ}=\left(m-3\right)^2+4m\)
\(=m^2-6m+9+4m\)
\(=m^2-2m+1+8=\left(m-1\right)^2+8>0\)
Do đó: PT luon có hai nghiệm phân biệt
\(\dfrac{2}{x_1}+\dfrac{2}{x_2}=\dfrac{2x_1+2x_2}{x_1x_2}=\dfrac{2\cdot\left(-m+3\right)}{-m}=\dfrac{-2m+6}{-m}\)
\(\dfrac{4x_2}{x_1}+\dfrac{4x_1}{x_2}=\dfrac{4\left(x_1^2+x_2^2\right)}{x_1x_2}\)
\(=\dfrac{4\left(x_1+x_2\right)^2-8x_1x_2}{x_1x_2}=\dfrac{4\left(-m+3\right)^2-8\cdot\left(-m\right)}{-m}\)
\(=\dfrac{4\left(m-3\right)^2+8m}{-m}\)
\(=\dfrac{4m^2-24m+36+8m}{-m}=\dfrac{4m^2-16m+36}{-m}\)
c: \(A=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}+1\)
\(=\sqrt{\left(-m+3\right)^2-4\cdot\left(-m\right)}+1\)
\(=\sqrt{m^2-6m+9+4m}+1\)
\(=\sqrt{m^2-2m+1+8}+1\)
\(=\sqrt{\left(m-1\right)^2+8}+1\ge2\sqrt{2}+1\)
Dấu '=' xảy ra khi m=1

pt có \(\Delta\)= (4m+1)2-4.2.(m-1) = 16m2+8m+1-8m+8=16m2+9 >0
==> pt có ngiệm với mọi m
theo hthuc vi ét ta có :\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-4m-1}{2}\\x1.x2=\dfrac{m-1}{2}\end{matrix}\right.\)(1)
mà có \(\dfrac{x1^2x2+x1x2^2}{x1^2+x2^2}=2==>\dfrac{x1.x2.\left(x1+x2\right)}{\left(x1+x2\right)^2-2x1x2}=2\) (2)
thay (1) vào (2) ta đc ........
giải ra m ( bạn tự lm nhé )
thay

\(\Delta=\left(m-2\right)^2-4.\left(5\right)=\left(m-2\right)^2-20\)
phương trình có 2 nghiệm phân biệt \(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow\left(m-2\right)^2-20>0\) \(\Leftrightarrow\left(m-2\right)^2>20\Leftrightarrow\left\{{}\begin{matrix}m-2>\sqrt{20}\\hoặc\\m-2< -\sqrt{20}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>2+\sqrt{20}\\hoặc\\m< 2-\sqrt{20}\end{matrix}\right.\)
áp dụng hệ thức vi ét ta có : \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=5\end{matrix}\right.\)
ta có : \(A=3\left(x_1^2+x_2^2\right)+8x_1x_2\)
\(A=3\left(\left(x_1+x_2\right)^2-2x_1x_2\right)+8x_1x_2\)
\(A=3\left(x_1+x_2\right)^2-6x_1x_2+8x_1x_2\)
\(A=3\left(x_1+x_2\right)^2+2x_1x_2\)
\(A=3\left(m-2\right)^2+2\left(5\right)\)
\(A=3\left(m-2\right)^2+10\ge10\forall m\)
\(\Rightarrow minA=10\Leftrightarrow3\left(m-2\right)^2=0\Leftrightarrow m-2=0\Leftrightarrow m=2\left(khôngthỏamảngđiềukiện\right)\)
vậy không có giá trị nào của m để A min
\(\Delta=\left(m-2\right)^2-4\left(m-5\right)=m^2-4m+4-4m+20\)
\(\Delta=m^2-8m+24=m^2-8m+16+8=\left(m-4\right)^2+8>0\forall m\)
vậy phương trình có 2 nghiệm phân biệt \(\forall m\)
áp dụng hệ thức vi ét ta có \(\left\{{}\begin{matrix}x_1+x_2=m-2\\x_1x_2=m-5\end{matrix}\right.\)
ta có : \(A=3\left(x_1^2+x_2^2\right)+8x_1x_2=3\left(\left(x_1+x_2\right)^2-2x_1x_2\right)+8x_1x_2\)
\(A=3\left(x_1+x_2\right)^2-6x_1x_2+8x_1x_2=3\left(x_1+x_2\right)^2+2x_1x_2\)
\(A=3\left(m-2\right)^2+2\left(m-5\right)=3\left(m^2-4m+4\right)+2m-10\)
\(A=3m^2-12m+12+2m-10=3m^2-10m+2\)
\(A=3m^2-2.\sqrt{3}m.\dfrac{10}{2\sqrt{3}}+\dfrac{100}{12}-\dfrac{100}{12}+2\)
\(A=\left(\sqrt{3}m-\dfrac{10}{2\sqrt{3}}\right)^2+\dfrac{-19}{3}\ge\dfrac{-19}{3}\)
\(\Rightarrow minA=\dfrac{-19}{3}khi\left(\sqrt{3}m-\dfrac{10}{2\sqrt{3}}\right)^2=0\)
\(\Leftrightarrow\sqrt{3}m-\dfrac{10}{2\sqrt{3}}=0\Leftrightarrow\sqrt{3}m=\dfrac{10}{2\sqrt{3}}\Leftrightarrow m=\dfrac{10}{6}\)
vậy \(minA=\dfrac{-19}{3}khi\) \(x=\dfrac{10}{6}\)

Để pt có nghiệm thì \(\Delta=1-4m\ge0\Rightarrow m\le\frac{1}{4}\)
Ta có:\(x_1=\frac{-1+\sqrt{1-4m}}{2};x_2=\frac{-1-\sqrt{1-4m}}{2}\)
\(\Rightarrow\hept{\begin{cases}x_1+x_2=-1\\x_1x_2=m\end{cases}}\)
\(\Rightarrow x_1^2\left(x_1+1\right)+x^2_2\left(x_2+1\right)=m\le\frac{1}{4}\)

a)Ta có \(\Delta=m^2-4m+4=\left(m-2\right)^2\ge0\)
=>pt luôn có 2 nghiệm
Vì pt có dạng a+b+c=0 nên pt sẽ có 1 nghiệm x1=1;x2=m-1
\(\Rightarrow M=\frac{x_2^2}{x_2^2+x_2}=\frac{x_2}{x_2+1}=\frac{m-1}{m}\)
b)Để \(M>0\) thì \(\frac{m-1}{m}>0\)
\(\Leftrightarrow1-\frac{1}{m}>0\Leftrightarrow1>\frac{1}{m}\)
\(\Leftrightarrow m>1\)

đây lại là ba cái đenta ;P;rồi thì S đó bạn !cả 2 nghiệm cùng âm dương jj đó tra mạng ra ngay mà

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16

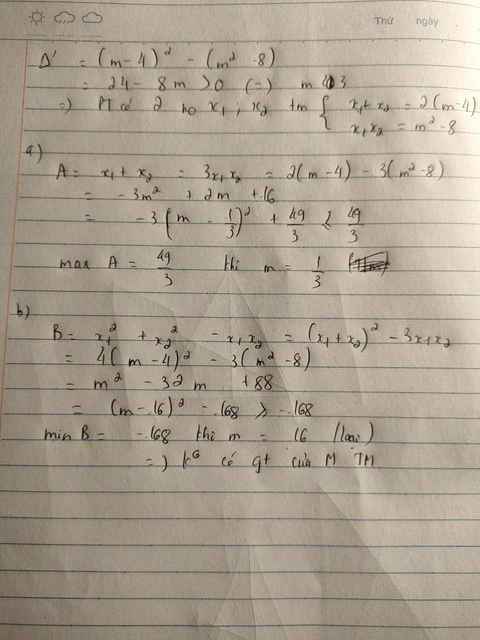
\(x^2-x\left(m+2\right)-m-3=0\)
Ta có \(\Delta=\left(m+2\right)^2-4\cdot\left(-m-3\right)\ge0\)
\(\Leftrightarrow m^2+8m+16\ge0\)
\(\Leftrightarrow\left(m+4\right)^2\ge0\) ( luôn đúng )
Theo định lý Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=m+2\\x_1x_2=-m-3\end{matrix}\right.\)
Khi đó \(A=-x_1^2x_2-x_1x_2^2=-x_1x_2\left(x_1+x_2\right)=\left(m+2\right)\left(m+3\right)\)
\(A=m^2+5m+6\)
\(A=\left(m+\frac{5}{2}\right)^2-\frac{1}{4}\ge\frac{-1}{4}\forall m\)
Vậy \(A_{min}=\frac{-1}{4}\Leftrightarrow m=\frac{-5}{2}\)