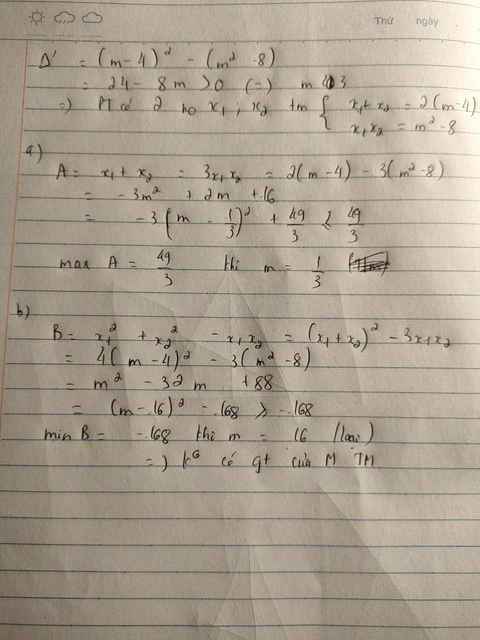Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để pt có nghiệm thì \(\Delta=1-4m\ge0\Rightarrow m\le\frac{1}{4}\)
Ta có:\(x_1=\frac{-1+\sqrt{1-4m}}{2};x_2=\frac{-1-\sqrt{1-4m}}{2}\)
\(\Rightarrow\hept{\begin{cases}x_1+x_2=-1\\x_1x_2=m\end{cases}}\)
\(\Rightarrow x_1^2\left(x_1+1\right)+x^2_2\left(x_2+1\right)=m\le\frac{1}{4}\)

đây lại là ba cái đenta ;P;rồi thì S đó bạn !cả 2 nghiệm cùng âm dương jj đó tra mạng ra ngay mà

Xét \(\Delta=1-4m\ge0\Rightarrow m\le\frac{1}{4}\)
Áp dụng Viete ta có:\(x_1+x_2=-1;x_1x_2=m\)
\(Q=x_1^2\left(x_1+1\right)+x_2^2\left(x_2+1\right)\)
\(=x_1^3+x_1^2+x_2^3+x_2^2\)
\(=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)+\left(x_1+x_2\right)^2-2x_1x_2\)
\(=-1^3-3\cdot m\cdot\left(-1\right)+\left(-1\right)^2-2m\)
\(=-1+3m+1-2m\)
\(=m\le\frac{1}{4}\)
Đẳng thức xảy ra khi m=1/4

\(\Delta'=\left[-\left(m+4\right)\right]^2-1\left(m^2-8\right)=m^2+8m+16-m^2+8=8m+24\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Leftrightarrow8m+24\ge0\Leftrightarrow m\ge-3\)
Áp dụng định lý Vi-ét ta có:\(\left\{{}\begin{matrix}x_1+x_2=2m+8\\x_1x_2=m^2-8\end{matrix}\right.\)
\(A=x^2_1+x^2_2-x_1-x_2\\ =\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)\\ =\left(2m+8\right)^2-2\left(m^2-8\right)-\left(2m+8\right)\\ =4m^2+32m+64-2m^2+16-2m-16\\ =2m^2+30m+64\)
Amin=\(-\dfrac{97}{2}\)\(\Leftrightarrow m=-\dfrac{15}{2}\)
\(B=x^2_1+x^2_2-x_1x_2\\ =\left(x_1+x_2\right)^2-3x_1x_2\\ =\left(2m+8\right)^2-3\left(m^2-8\right)\\ =4m^2+32m+64-3m^2+24\\ =m^2+32m+88\)
Bmin=-168\(\Leftrightarrow\)m=-16

\(\Delta'=\left(a-1\right)^2-\left(a^2+a-2\right)=-3a+3\)
Để phương trình có hai nghiệm \(x_1;x_2\) thì \(\Delta'\ge0\Leftrightarrow-3a+3\ge0\Leftrightarrow a\le1\)
Áp dụng hệ thức Viet ta có: \(\hept{\begin{cases}x_1+x_2=2\left(a-1\right)\\x_1.x_2=a^2+a-2\end{cases}}\)
Vậy thì \(P=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1.x_2=4\left(a-1\right)^2-2\left(a^2+a-2\right)\)
\(=2a^2-10a+8=2\left(a^2-5a+\frac{25}{4}\right)-\frac{9}{2}=2\left(a-\frac{5}{2}\right)^2-\frac{9}{2}\ge-\frac{9}{2}\)
Vậy \(\text{min}P=-\frac{9}{2}\Leftrightarrow a=\frac{5}{2}.\)
Bài giải :
Δ'=(a−1)2−(a2+a−2)=−3a+3
Để phương trình có hai nghiệm x1;x2 thì Δ'≥0⇔−3a+3≥0⇔a≤1
Áp dụng hệ thức Viet ta có: {
| x1+x2=2(a−1) |
| x1.x2=a2+a−2 |
Vậy thì P=x12+x22=(x1+x2)2−2x1.x2=4(a−1)2−2(a2+a−2)
=2a2−10a+8=2(a2−5a+254 )−92 =2(a−52 )2−92
Với a≤1⇒P≥0
Vậy minP = 0 khi a = 1.

Xét pt (1) có:
\(\Delta=\left(-2m\right)^2-4\left(m-2\right)\)
= \(4m^2-4m+8\)
= \(\left(2m-1\right)^2+7>0\)
\(\Rightarrow\) Pt (1) luôn có 2 nghiệm phân biệt với mọi m
Áp dụng hệ thức Vi-ét ta có:
\(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1.x_2=m-2\end{matrix}\right.\)
Theo đề bài ta có:
\(\left(1+x_1\right)\left(2-x_2\right)+\left(1+x_2\right)\left(2-x_1\right)=x_1^2+x_2^2+2\)
\(\Leftrightarrow2-x_2+2x_1-x_1x_2+2-x_1+2x_2-x_1x_2=\left(x_1+x_2\right)^2-2x_1x_2+2\) \(\Leftrightarrow-\left(x_1+x_2\right)+2\left(x_1+x_2\right)+2-\left(x_1+x_2\right)^2=0\)
\(\Leftrightarrow-\left(x_1+x_2\right)\left[1-2+\left(x_1+x_2\right)\right]+2=0\)
\(\Leftrightarrow-2m\left(2m-1\right)+2=0\)
\(\Leftrightarrow-4m^2+2m+2=0\)
\(\Leftrightarrow\left(m-1\right)\left(2m+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m-1=0\\2m+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=1\\m=\dfrac{-1}{2}\end{matrix}\right.\)
Vậy để pt (1) có 2 nghiệm \(x_1,x_2\) thỏa mãn \(\left(1+x_1\right)\left(2-x_2\right)+\left(1+x_2\right)\left(2-x_1\right)=x_1^2+x_2^2+2\) thì \(m=1\) hoặc \(m=\dfrac{-1}{2}\)
\(\Delta\)' = m2 - m + 2 = m2 - 2.m.\(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) - \(\dfrac{1}{4}\) + 2 = \(\left(m-\dfrac{1}{2}\right)^2\) + \(\dfrac{7}{4}\) \(\ge\) \(\dfrac{7}{4}\) > 0
\(\Rightarrow\) phương trình luôn có 2 nghiệm \(\forall\)m
áp dụng hệ thức vi ét ta có : \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1.x_2=m-2\end{matrix}\right.\)
(1 + x1)(2 - x2) + (1 + x2)(2 - x1) = x12 + x22 + 2
2 - x2 + 2x1 - x1x2 + 2 - x1 + 2x2 - x1x2 = (x1 + x2)2 - 2x1x2 + 2
= (x1 + x2)2 - (x1 + x2) - 2 = 0
thay vào ta có : (2m)2 - 2m - 2 = 0
4m2 - 2m - 2 = 0 ta có : a + b + c = 4 - 2 - 2 = 0
\(\Rightarrow\) phương trình có 2 nghiệm phân biệt
m1 = 1 ; m2 = \(\dfrac{c}{a}\) = \(-\dfrac{1}{2}\)
vậy m = 1 ; m = \(-\dfrac{1}{2}\) thảo mảng điều kiện bài toán

Ta có: \(\frac{c}{a}=-\frac{2}{2}=-1< 0\)
=> Phương trình luôn có 2 ngiệm trái dấu \(x_1;x_2\)
Theo định lí viet: \(x_1x_2=-1;x_1+x_2=\frac{1-m}{2}\)
Ta có: \(\left(x_1+\frac{1}{2}x^2_1-x^3_1\right)\left(x_2+\frac{1}{2}x^2_2-x^3_2\right)=4\)
<=> \(x_1x_2\left(x_1^2-\frac{1}{2}x_1-1\right)\left(x_2^2-\frac{1}{2}x_2-x_2\right)=4\)
<=> \(\left(2x_1^2-x_1-2\right)\left(2x_2^2-x_2-2\right)=-16\)
<=> \(\left(2x_1x_2\right)^2-2x_1^2x_2-4x_1^2-2x_1x_2^2+x_1x_2+2x_2-4x_2^2+2x_2+4=-16\)
<=> \(4+2x_1-4x_1^2+2x_2-1+2x_2-4x_2^2+2x_2+4=-16\)
<=> \(4x_1^2+4x_2^2-4x_1-4x_2=23\)
<=> \(4\left(x_1+x_2\right)^2-4\left(x_1+x_2\right)=15\)
<=> \(\orbr{\begin{cases}x_1+x_2=\frac{5}{2}\\x_1+x_2=-\frac{3}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{1-m}{2}=\frac{5}{2}\\\frac{1-m}{2}=-\frac{3}{2}\end{cases}}\Leftrightarrow\orbr{\begin{cases}m=-4\\m=4\end{cases}}\)
Vậy:....