Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, xét \(\Delta ABC\) vuông tại A áp dụng hệ thức lượng\(=>AC^2=CH.BC=>HC=\dfrac{AC^2}{BC}=\dfrac{12^2}{15}=9,6cm\)
\(=>HB=BC-HC=15-9,6=5,4cm\)
áp dụng Pytago trong \(\Delta AHC\) vuông tại H
\(=>HA=\sqrt{AC^2-HC^2}=\sqrt{12^2-9,6^2}=7,2cm\)
\(b,\) do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
\(=>\left\{{}\begin{matrix}EH\perp AB\\HF\perp AC\end{matrix}\right.\) mà \(\Delta AHB\) và \(\Delta AHC\) lần lượt vuông góc tại H
theo hệ thức lượng
\(=>\left\{{}\begin{matrix}AH^2=AE.AB\\AH^2=AF.AC\end{matrix}\right.\)=>\(AE.AB=AF.AC\)
c, do E,F là hình chiếu vuông góc của H lần lượt lên AB, AC
=> tứ giác EHFA là hình chữ nhật\(=>AE=HF< =>HF^2=AE^2\)
áp dụng pytago trong \(\Delta EHA\) vuông tại E
\(=>HE^2+AE^2=AH^2< =>HE^2+HF^2=AH^2\)(1)
theo hệ thức lượng trong tam giác ABC vuông tại A đường cao AH
\(=>AH^2=HB.HC\left(2\right)\)
(1)(2)=>\(HE^2+HF^2=HB.HC\)

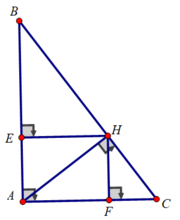
b) Xét tam giác ABH vuông tại H có HE là đường cao
⇒ AE.AB = AH2 (1)
Xét tam giác AHC vuông tại H có HF là đường cao
⇒ AF.AC = A H 2 (2)
Từ (1) và (2) ⇒ AE.AB = AF.AC

b: Xét ΔAHB vuông tại H có HD là đường cao
nên \(AD\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HE là đường cao
nên \(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)

a, tứ giác EHFA có : góc A= góc E = góc F =90 độ ( GT )
=>> EHFA là HCN
=>> AH = EF ( hai đường chéo HCN )
b, mình hơi vội nên mình gợi ý cho bạn câu b thế này ạ ! CM tam giác BAC ~ tam giác EAF
=>> AE/AF=AC/AB
=>> AE.AB=AF.AC
kẻ hộ mình cái hình
a)Xét tứ giác AEHF có góc A=góc E = góc F= 90 độ nên AEHF là hình chữ nhật
Do đó AH=EF theo tính chất 2 đường chéo của hcn
b)chưa có hình chưa làm được

b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HD là đường cao ứng với cạnh huyền AB, ta được:
\(AD\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AD\cdot AB=AE\cdot AC\)