Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)

(*) mk mới hok dạng toán này trên mạng ; nên lm thử thôi nha bn
hình :
A B C D F E O
a) ta có : \(VT=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}+\overrightarrow{OE}+\overrightarrow{OF}\)
\(=\overrightarrow{OA}+\overrightarrow{EO}+\overrightarrow{OC}+\overrightarrow{AO}+\overrightarrow{OE}+\overrightarrow{CO}\)
\(=\left(\overrightarrow{AO}+\overrightarrow{OA}\right)+\left(\overrightarrow{CO}+\overrightarrow{OC}\right)+\left(\overrightarrow{EO}+\overrightarrow{OE}\right)\)
\(=\overrightarrow{AA}+\widehat{CC}+\overrightarrow{EE}=\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}=VP\left(đpcm\right)\)
b) ta có : \(VT=\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{OE}=\overrightarrow{FO}+\overrightarrow{OE}-\overrightarrow{AO}\)
\(=\overrightarrow{FE}-\overrightarrow{FE}=\overrightarrow{EE}=\overrightarrow{0}=VP\left(đpcm\right)\)
c) ta có : \(VT=\overrightarrow{AB}+\overrightarrow{AO}+\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{AF}+\overrightarrow{FE}\)
\(=\overrightarrow{AB}+\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AD}=VP\left(đpcm\right)\)
d) ta có : \(VT=\overrightarrow{MA}+\overrightarrow{MC}+\overrightarrow{ME}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}+\overrightarrow{MF}+\overrightarrow{FE}\)
\(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\left(\overrightarrow{BA}+\overrightarrow{DC}+\overrightarrow{FE}\right)\)
\(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\left(\overrightarrow{BA}+\overrightarrow{FE}+\overrightarrow{EO}\right)\) \(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\left(\overrightarrow{BA}+\overrightarrow{FO}\right)\) \(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\left(\overrightarrow{BA}-\overrightarrow{OF}\right)\) \(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\left(\overrightarrow{BA}-\overrightarrow{BA}\right)\) \(=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\overrightarrow{AA}=\left(\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}\right)+\overrightarrow{0}\) \(=\overrightarrow{MB}+\overrightarrow{MD}+\overrightarrow{MF}=VP\left(đpcm\right)\)

1)\(VT=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\overrightarrow{CO}+\overrightarrow{DO}+\overrightarrow{OC}+\overrightarrow{OC}=\overrightarrow{CO}+\overrightarrow{OC}+\overrightarrow{DO}+\overrightarrow{OD}=\overrightarrow{0}\)
2)\(VT=\overrightarrow{DA}-\overrightarrow{DB}+\overrightarrow{DC}=\overrightarrow{BA}+\overrightarrow{DC}=\overrightarrow{0}\)
3)\(VT=\overrightarrow{DO}+\overrightarrow{AO}=\overrightarrow{OB}+\overrightarrow{AO}=\overrightarrow{AB}\)
4)\(\overrightarrow{MA}+\overrightarrow{MC}=\overrightarrow{MB}+\overrightarrow{BA}+\overrightarrow{MD}+\overrightarrow{DC}=\overrightarrow{MB}+\overrightarrow{MD}\left(đpcm\right)=\overrightarrow{MO}+\overrightarrow{OB}+\overrightarrow{MO}+\overrightarrow{OD}=2\overrightarrow{MO}\left(đpcm\right)\)
Chúc bạn học tốt!!!!!
Đăng kí kênh Youtube 'Ban Mai Anime' giúp mình nhé!!!!

a) Ta có:
\(\overrightarrow{AB'}+\overrightarrow{AC'}=\overrightarrow{BC}+\overrightarrow{AB}+\overrightarrow{BC'}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\)\(=\overrightarrow{AC}+\overrightarrow{CA}=\overrightarrow{0}\).
Vậy A là trung điểm của B'C'.
b)
A B C B' C' A'
Theo câu a ta chứng minh được A là trung điểm của B'C'.
Tương tự ta chứng minh được: B là trung điểm của A'C'; C là trung điểm của A'B'.
Từ đó suy ra ba đường thẳng AB', BB', CC' là ba đường trung tuyến của tam giác A'B'C' nên ba đường thẳng AA', BB', CC' đồng quy.
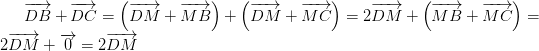
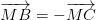
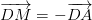
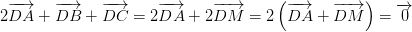
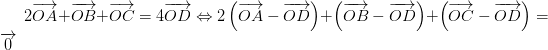
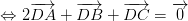 luôn đúng theo câu a
luôn đúng theo câu a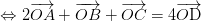 , với O là điểm tùy ý
, với O là điểm tùy ý
Do \(\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên hai véc tơ \(\overrightarrow{a}\) và \(\overrightarrow{b}\) đối nhau.
a)
\(\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên O là trung điểm của AB.
b) \(\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}=\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{0}\) nên \(O\equiv B\).