Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(\overrightarrow{AM}+\overrightarrow{BN}=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{AC}\)
b: \(=\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
\(=\overrightarrow{AC}+\dfrac{1}{2}\overrightarrow{BA}\)
c: \(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}\)
\(=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{BC}+\dfrac{1}{2}\overrightarrow{CA}\)
\(=\dfrac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)=\overrightarrow{0}\)

câu 2 ( các kí hiệu vecto khi lm bài thỳ b tự viết nhé mk k viết kí hiệu để trả lời cho nhanh hỳ hỳ )
OA+ OB + OC = OA'+ OB' + OC'
<=> OA - OA' + OB - OB' + OC - OC' = 0
<=> A'A + B'B + C'C = 0
<=> 2 ( BA + CB + AC ) = 0
<=> 2 ( CB + BA + AC ) = 0
<=> 2 ( CA + AC ) = 0
<=> 0 = 0 ( luôn đúng )
câu 1 ( các kí hiệu vecto b cx tự viết nhá )
VT = OD + OC = OA + AD + OB + BC = OA + OB + AD + BC = BO + OB + AD + BC = 0 + AD + BC = AD + BC = VP ( đpcm)

a/ \(VT=\overrightarrow{AB}+\overrightarrow{BF}+\overrightarrow{BC}+\overrightarrow{CG}+\overrightarrow{CD}+\overrightarrow{DH}+\overrightarrow{DA}+\overrightarrow{AE}\)
\(=\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DA}\right)+\left(\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{2}\overrightarrow{DA}+\frac{1}{2}\overrightarrow{AB}\right)\)
\(=\overrightarrow{0}+\frac{1}{2}.\overrightarrow{0}=\overrightarrow{0}=VP\)
b/ Câu này áp dụng luôn kq câu a
\(\overrightarrow{MF}-\overrightarrow{MA}+\overrightarrow{MG}-\overrightarrow{MB}+\overrightarrow{MH}-\overrightarrow{MC}+\overrightarrow{ME}-\overrightarrow{MD}=\overrightarrow{0}\)
chuyển mấy cái vecto kia sang vế phải là có ngay đpcm câu b
c/\(VT=\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{AI}+\overrightarrow{IC}+\overrightarrow{AI}+\overrightarrow{ID}=3\overrightarrow{AI}+\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}\)
Để ý tới G là TĐ CD, F là TĐ BC
Theo quy tắc trung điểm
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}=2\overrightarrow{IF}=2\overrightarrow{HI}\)
\(\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=2\overrightarrow{HI}+\overrightarrow{ID}=\overrightarrow{HI}+\overrightarrow{HD}\)
Mà \(\overrightarrow{HD}=\overrightarrow{AH}\Rightarrow\overrightarrow{IB}+\overrightarrow{IC}+\overrightarrow{ID}=\overrightarrow{HI}+\overrightarrow{AH}=\overrightarrow{AI}\)
Thay vào cái trên sẽ có đpcm

a)Ta có:
\(\overrightarrow{OA}+\overrightarrow{OM}+\overrightarrow{ON}=\overrightarrow{CO}+\dfrac{1}{2}\left(\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OC}+\overrightarrow{OD}\right)\)
\(=\overrightarrow{CO}+\dfrac{1}{2}.2\overrightarrow{OC}\)
\(=\overrightarrow{0}\)
\(\RightarrowĐPCM\)
b) Ta có:
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AD}+2\overrightarrow{AB}\right)\)
\(\Rightarrow2\overrightarrow{AM}=\overrightarrow{AD}+2\overrightarrow{AB}\) (1)
Mà \(2\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{AC}\)(2)
Từ (1)(2) =>\(\overrightarrow{AD}+2\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{AC}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\RightarrowĐPCM\)
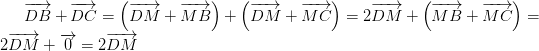
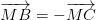
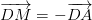
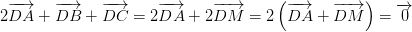
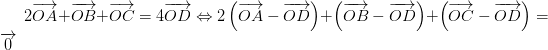
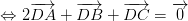 luôn đúng theo câu a
luôn đúng theo câu a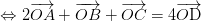 , với O là điểm tùy ý
, với O là điểm tùy ý