Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 9: Khẳng định nào sau đây
A . Hai góc bằng nhau là hai góc đối đỉnh.
B. Đường trung trực của đoạn thẳng thì đi qua trung điểm của đoạn thẳng ấy.
C. Hai đường thẳng không cắt nhau thì song song.
D. Đường trung trực của một đoạn thẳng là đường vuông góc với đoạn thẳng đó.
.Câu 10: Trong các phát biểu sau đây thì phát biểu nào đúng?
A. Hai tia phân giác của cặp góc bù nhau thì vuông góc với nhau.
B. Hai tia phân giác của cặp góc kề nhau thì vuông góc với nhau.
C. Hai tia phân giác của cặp góc đối đỉnh thì vuông góc với nhau.
D. Hai tia phân giác của cặp góc kề bù thì vuông góc với nhau.

2 TG IBA = tg ICA(c-g-c)
2 TG IMA=TG INA(c-g-c) (1)
Các cặp cạnh bằng nhau:
AM=BM vì M là trung điểm của AB
AN=CN vì N là trung điểm của AB
AB=AC vì Tam giác ABC cân.
MI=NI vì (1)
Các góc bằng nhau:
AIB = AIC do AI là đường cao của tam giác ABC.
CBA = BCA vì tam giác ABC cân
IAB=IAC vì tg IBA=ICA
IMA=INA vì (2)
IMB=INC vì góc IMA=INA,mà 2 góc IMB kề bù IMA,INC kề bù INA.
Các góc bằng 90*: BIA và CIA

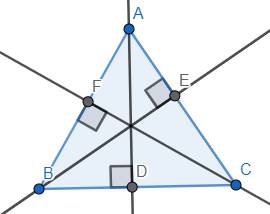
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.
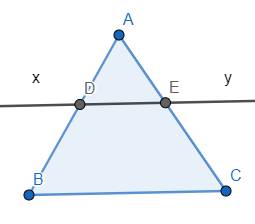
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)
Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)
Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.
Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM
a. Ta có:
∠NAQ và ∠PAM là hai góc đối đỉnh
Suy ra:∠NAQ = CPAM
mà ∠PAM = 33o nên ∠NAQ = 33o
b. ∠PAM và ∠MAQ là hai góc kề bù nên ∠PAM + ∠MAQ=180o
Suy ra: ∠MAQ = 180o-∠PAM =180o-33o=147o
c. Các cặp góc đối đỉnh là: ∠PAM và ∠NAQ ; ∠PAN và ∠MAQ
d. Các cặp góc kề bù là: ∠PAM và ∠MAQ; ∠PAM và ∠PAN ; ∠NAQ và ∠PAN ; ∠NAQ và ∠QAM

Bạn tự vẽ hình nhé !!!
- TA có : \(\widehat{AMC}=\widehat{BMD}=30\)độ ( Đối đỉnh )
Vì góc AMD và góc BMD kề bù nên :
<=> Góc AMD + góc BMD = 180 độ
<=> góc AMD = 150 độ
b) Cặp đóc đối đỉnh : góc AMC và BMD
góc AMD và BMC
Cặp góc bù nhau : góc ACM và AMD
góc BMD và BMC


a: Xét tứ giác ADBC có
AB và CD cắt nhau tại trung điểm của mỗi đường
Do đó: ADBC là hình bình hành
Suy ra: AD=BC; AC=BD
Xét ΔABC và ΔBAD có
AB chung
BC=AD
AC=BD
Do đó: ΔABC=ΔBAD
Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
b: CA//DB
CB//AD