Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

ĐK: xOy khác 180o
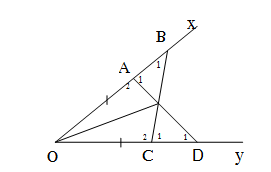
Ta có hình vẽ:
x y O D E B D K
Xét Δ DOC và Δ EOB có:
OD = OE (gt)
O là góc chung
OC = OB (gt)
Do đó, Δ DOC = Δ EOB (c.g.c)
=> CD = BE (2 cạnh tương ứng)
DCO = EBO (2 góc tương ứng)
ODC = OEB (2 góc tương ứng)
Mà ODC + BDC = 180o (kề bù)
OEB + BEC = 180o (kề bù)
nên BDC = BEC
Có: OC = OB (gt)
OD = OE (gt)
=> OC - OE = OB - OD
=> EC = BD
Xét Δ DBK và Δ ECK có:
DBK = ECK (cmt)
BD = EC (cmt)
BDK = CEK (cmt)
Do đó, Δ DBK = Δ ECK (g.c.g)
=> DK = KE (2 cạnh tương ứng) (đpcm)

1) Xét Δ DOC và Δ EOB có:
OD = OE (Gt)
Góc O : chung
OB = OC (Gt)
=> Δ DOC = Δ EOB (c.g.c)
2)=> CD = BE (2 cạnh tương ứng)
=>\(\widehat{\text{DCO}}\) = \(\widehat{\text{EBO}}\) (2 góc tương ứng)
=>\(\widehat{\text{ODC}}\) = \(\widehat{\text{OEB }}\) (2 góc tương ứng)
Mà \(\widehat{\text{ODC}}\) + \(\widehat{\text{BDC}}\) = 180 (kề bù)
\(\widehat{\text{OEB }}\) + \(\widehat{\text{BEC}}\) = 180 (kề bù)
=> \(\widehat{\text{BDC}}\) = \(\widehat{\text{BEC}}\)
Có: OC = OB (gt)
OD = OE (gt)
=> OC - OE = OB - OD
=> EC = BD
Xét Δ DBK và Δ ECK có:
\(\widehat{\text{DBK}}\) = \(\widehat{\text{ECK}}\) (cmt)
BD = EC (cmt)
\(\widehat{\text{BDK}}\) = \(\widehat{\text{CEK}}\) (cmt)
=> Δ DBK = Δ ECK (g.c.g)
=> DK = KE (2 cạnh tương ứng)
3)=>BK = CK (2 cạnh tương ứng)
Xét Δ DKO và Δ EKO có:
OD = OE (Gt)
Cạnh OK : chung
KD = KE (cmt)
=> Δ DKO và Δ EKO (c.c.c)
=> \(\widehat{\text{DOK}}\) = \(\widehat{\text{EOK}}\) (2 góc tương ứng)
=> OK là tia phân giác của góc xOy
Xét Δ BKO và Δ CKO có:
OB = OC (Gt)
Cạnh OM : chung
MB = MC (M là tia phân giác của BC)
=> Δ BMO và Δ CMO (c.c.c)
=> \(\widehat{\text{BOM}}\) = \(\widehat{\text{COM}}\) (2 góc tương ứng)
=> OM là tia phân giác của góc xOy
Mà OK là tia phân giác của góc xOy
=> 3 điểm O ;K ;M thẳng hàng

Chép lại đề: (vì đề của bạn có chút sai sót)
Cho \(\widehat{xOy}\) khác góc bẹt. Lấy A, B thuộc Ox sao cho OA < OB. Lấy C, D thuộc Oy sao cho OC = OA; OD = OB. Gọi E là giao điểm của AD và BC. CMR:
a, AD = BC
b, Tam giác AEB = tam giác CED
c, OE là tia phân giác của \(\widehat{xOy}\)
Ta có hình vẽ:
a/ Xét tam giác OAD và tam giác OBC có
OA = OC (GT)
\(\widehat{O}\): góc chung
OB = OD (GT)
Vậy tam giác OAD = tam giác OBC (c.g.c)
=> AD = BC (2 cạnh tương ứng) (đpcm)
b/ Xét tam giác AEB và tam giác CED có:
\(\widehat{B}\)=\(\widehat{D}\) (vì tam giác OAD = tam giác OBC) (1)
OA = OC; OB = OD => AB = CD (2)
Ta có: \(\Delta\)OAD = \(\Delta\)OBC
=> \(\widehat{OAD}\)=\(\widehat{OCB}\) (2 góc tương ứng) (*)
Ta có: \(\widehat{OAD}\)+\(\widehat{DAB}\)=1800 (kề bù) (**)
\(\widehat{OCB}\) + \(\widehat{BCD}\) = 1800 (kề bù) (***)
Từ (*), (**), (***) \(\Rightarrow\)\(\widehat{DAB}\)=\(\widehat{BCD}\)(3)
Từ (1), (2), (3) => tam giác AEB = tam giác CED (g.c.g) (đpcm)
c/ Xét tam giác OBE và tam giác ODE có:
OB = OD (GT)
OE: cạnh chung
BE = EC (vì tam giác AEB = tam giác CED)
Vậy tam giác OBE = tam giác ODE (c.c.c)
=> \(\widehat{BOE}\)=\(\widehat{DOE}\) (2 góc tương ứng)
=> OE là phân giác góc xOy (đpcm)
Vậy OE là tia phân giác \(\widehat{xOy}\)

x O y E A B C D 1 2 1 1 1 1 1 2
Giải:
a) Xét \(\Delta OAD,\Delta OCB\) có:
\(OA=OC\left(gt\right)\)
\(\widehat{O}\): góc chung
\(OD=OB\left(gt\right)\)
\(\Rightarrow\Delta OAD=\Delta OCB\left(c-g-c\right)\)
\(\Rightarrow AD=CB\) ( cạnh t/ứng )
\(\Rightarrow\widehat{B_1}=\widehat{D_1}\) ( góc t/ứng )
b) Ta có: OB = OD
OA = OC
\(\Rightarrow OB-OA=OD-OC\)
\(\Rightarrow AB=CD\)
Ta có: \(\widehat{A_1}+\widehat{B_1}+\widehat{E_1}=180^o\)
\(\widehat{C_1}+\widehat{E_2}+\widehat{D_1}=180^o\)
Mà \(\widehat{B_1}=\widehat{D_1}\) ( theo phần a ); \(\widehat{E_1}=\widehat{E_2}\) ( đối đỉnh )
\(\Rightarrow\widehat{A_1}=\widehat{C_1}\)
Xét \(\Delta EAB,\Delta ECD\) có:
\(\widehat{A_1}=\widehat{C_1}\left(cmt\right)\)
AB = CB ( cmt )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(\Rightarrow\Delta EAB=\Delta ECD\left(g-c-g\right)\)
\(\Rightarrow EB=ED\) ( cạnh t/ứng )
c) Xét \(\Delta OBE,\Delta ODE\) có:
\(EB=ED\) ( theo phần b )
\(\widehat{B_1}=\widehat{D_1}\) ( theo phần a )
\(OB=OD\left(gt\right)\)
\(\Rightarrow\Delta OBE=\Delta ODE\left(c-g-c\right)\)
\(\Rightarrow\widehat{O_1}=\widehat{O_2}\)
\(\Rightarrow OE\) là tia phân giác của \(\widehat{xOy}\)
Vậy...

Giải:
a) ∆OAD và ∆OCB có:
OA= OC(gt)
∠O chung OB = OD (gt)
OAD = OCB (c.g.c) AD = BC
Nên ∆OAD=∆OCB (c.g.c) => AD=BC.
b) Ta có
∠A1 = 1800 – ∠A2
∠C1 = 1800 – ∠C2
∠A2 = ∠C2 do ΔOAD = ΔOCB (c/m trên)
⇒ ∠A1 = ∠C1
Ta có:
OB = OA + AB
OD = OC + CD
mà OB = OD, OA = OC
⇒ AB = CD
Xét ΔEAB = ΔECD có:
∠A1 = ∠C1 (c/m trên)
AB = CD (c/m trên)
∠B1 = ∠D1 (ΔOCB = ΔOAD)
⇒ ΔEAB = ΔECD (g.c.g)
c) Xét ΔOBE và ΔODE có:
OB = OD (GT)
OE chung
AE = CE (ΔAEB = ΔCED)
⇒ΔOBE = ΔODE (c.c.c)
⇒ ∠AOE = ∠COE
⇒ OE là phân giác của góc ∠xOy.

a: Xét ΔODC và ΔOBE có
OD=OB
\(\widehat{O}\) chung
OC=OE
Do đó: ΔODC=ΔOBE
Câu b và c đề sai rồi bạn

