Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Chứng minh tứ giác ABOC nội tiếp được đường tròn.
A B O ^ = 90 0 A C O ^ = 90 0 A B O ^ + A C O ^ = 180 0
=> tứ giác ABOC nội tiếp được đường tròn.
b) Vẽ cát tuyến ADE của (O) sao cho ADE nằm giữa 2 tia AO, AB; D, E Î (O) và D nằm giữa A, E. Chứng minh A B 2 = A D . A E .
Tam giác ADB đồng dạng với tam giác ABE
⇒ A B A E = A D A B ⇔ A B 2 = A D . A E
c) Gọi F là điểm đối xứng của D qua AO, H là giao điểm của AO và BC. Chứng minh: ba điểm E, F, H thẳng hàng.
Ta có D H A ^ = E H O ^
nên D H A ^ = E H O ^ = A H F ^ ⇒ A H E ^ + A H F ^ = 180 0 ⇒ 3 điểm E, F, H thẳng hàng.
Có 1 phần câu trả lời ở đây.
Giải toán: Bài hình trong đề thi HK2 Lớp 9 | Rất phức tạp. - YouTube

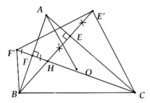
a, ∆CHE' cân tại C => C E ' H ^ = C H E ' ^
DBHF' cân tại B => B F ' H ^ = B H F ' ^
Mà => C H E ' ^ = B H F ' ^ (đối đỉnh)
=> C E ' H ^ = B F ' H ^
=> Tứ giác BCE'F' nội tiếp đường tròn tâm (O)
b, Có B F C ' ^ = B E ' C ^ = C H E ' ^ = C A B ^
Vậy A, F', E' cùng chắn BC dưới góc bằng nhau
=> 5 điểm B, F', A, E', C cùng thuộc một đường tròn tâm (O)
c, AF' = AE' (=AH) => AO là trung trực của EF => AO ^ E'F'. DHE'F' có EF là đường trung bình => EF//E'F'
=> AO ^ FE
d, A F H ^ = A E H ^ = 90 0 => AFHE nội tiếp đường tròn đường kính AH. Trong (O): Kẻ đường kính AD, lấy I trung điểm BC
=> OI = 1 2 AH, BC cố định => OI không đổi
=> Độ dài AH không đổi
=> Bán kính đường tròn ngoại tiếp ∆AEF không đổi

a: góc AMB=1/2*sđ cung AB=90 độ
góc BMD+góc BCD=180 độ
=>BMDC nội tiếp
b: Xét ΔAMB vuông tại M và ΔACD vuông tại C có
góc MAB chung
=>ΔAMB đồng dạng với ΔACD
=>AM/AC=AB/AD
=>AM*AD=AB*AC=6R^2
c: góc ADC=90-30=60 độ
/
a: B đối xứng A qua d
=>d là đường trung trực của AB
=>O nằm trên đường trung trực của AB
=>OA=OB
=>B thuộc (O)
C đối xứng A qua O
=>O là trung điểm của AC
=>OA=OC
=>C thuộc (O)
D đối xứng B qua O
=>O là trung điểm của BD
=>OB=OD
=>D nằm trên (O)
b: Xét tứ giác ABCD có
O là trung điểm chung của AC và BD
=>ABCD là hình bình hành
Hình bình hành ABCD có AC=BD
nên ABCD là hình chữ nhật
c: Ta có: OC=OD
=>O nằm trên đường trung trực của CD
Ta có: AB//CD
d\(\perp\)AB
Do đó: d\(\perp\)CD
mà d\(\supset\)O
và O nằm trên đường trung trực của CD
nên d là đường trung trực của CD
=>C đối xứng với D qua d