Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì tia Ot là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{xOt}=\widehat{yOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{70^o}{2}=35^o\)
Vậy \(\widehat{yOt}=35^o\)
b) Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox có :
\(\widehat{xOy}=70^o< \widehat{xOz}=90^o\)
=> Tia Oy nằm giữa tia Ox và tia Oz
=> \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\left(1\right)\)
Thay \(\widehat{xOy}=70^o\) và \(\widehat{xOz}=90^o\) vào (1) , ta được :
\(70^o+\widehat{yOz}=90^o\)
=> \(\widehat{yOz}=90^o-70^o=20^o\)
Vậy \(\widehat{yOz}=20^o\)
Cặp góc phụ nhau có trong hình là \(\widehat{xOy}\) và \(\widehat{yOz}\)

( Hình thì bạn tự vẽ )
a/ ta có góc xOy là góc nhọn
=> xOy < 90độ
=> MOx= MOy<45 độ (1) .
Mặt khác: Giả sử OA>MA
=> AMO > MOA <=> 180 - BMO>MOA
<=> 180 - (MOA + OAM)> MOA
<=> 180 -(MOA+90)>MOA
<=> 90>2MOA
<=>MOA<45
<=> MOx<45 (đúng do (1))
Vậy OA>MA
b/ Giả sử OB>OM .
Khi đó: OMB > OBM
<=> OMB>180 - OMB - MOB
<=> 2OMB>180-MOA
<=>2OMB>180-(90-OMA)
<=> 2OMB-OMA>90
<=> 2OMB-(180-OMB)>90
<=> 3OMB>270
<=> OMB>90 (đúng do OMB= OAM + AOM=90+AOM)
Vậy OB >OM
![]()

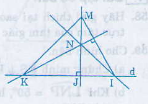
∆MKI có JM là đường cao (l ⊥ d), đường thẳng KN cũng là đường cao ( giả thiết KN ⊥ MI). Hai đường cao cắt nhau tại N nên N là trực tâm ∆MKI. Vậy NI ⊥ MK

câu a: do h thuộc đường phân giác góc xOy nên theo tính chất ta có HA = HB.(10
HA vuông góc với 0A,HB VUÔNG góc với OB,góc xOy=90 => HAOB là hcn=> góc AHB =90(2)
Từ (1) và (2)=>HAB là tam giác vuông cân tại H

xot= nhiu vay ban
de ko cho hay ban ghi thieu vay
de minh con giai nua
