Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Suất điện động cảm ứng trong ống dây :
ξ = - L\(\frac{\triangle I}{\triangle t}\) → | ξ | = L\(\left|\frac{\triangle I}{\triangle t}\right|\)
Với L = 0,004 H ; \(\triangle\)I = I1 - I2 = 1,2 - 0,4 = 0,8 ( A ) ; \(\triangle\)t = 0,2 s
Thế số vào ta có : ξ = 0,016 ( V )

Đáp án C
e = − L . Δ i Δ t = − 20.10 − 3 . − 1 − 1 10.10 − 3 = 4 V .

Thử coi ạ, sai bỏ qua nha :))
a/ \(E_{tc}=L.\frac{\left|\Delta i\right|}{\Delta t}=0,5.\frac{0,4}{0,15}=\frac{4}{3}\left(V\right)\)
b/ \(I=\frac{E_{tc}}{R}=\frac{\frac{4}{3}}{0,5}=\frac{8}{3}\left(A\right)\)

Bài 1:
a/ \(L=4\pi^2.10^{-7}.\dfrac{N^2}{l}S=4\pi^2.10^{-7}.\dfrac{1000^2}{0,3}.0,04^2.\pi=...\left(H\right)\)
b/ \(\phi=L.i=...\left(Wb\right)\)
c/ \(\xi=\dfrac{L.\Delta i}{\Delta t}=\dfrac{L.\left(2-0\right)}{0,1}=...\left(V\right)\)
2/
a/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow10=\dfrac{1}{0,3}+\dfrac{1}{d'}\Leftrightarrow d'=15\left(cm\right)\)
\(h'=\left|\dfrac{d'}{d}\right|.h=\left|\dfrac{15}{30}\right|.2=1\left(cm\right)\)
b/ Chắc là màn cố định nhỉ?
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'};\left|\dfrac{d'}{d}\right|=2\)
Vì cho ảnh rõ nét trên màn nên ảnh là ảnh thật và ngược chiều với vật
\(\Rightarrow\left|\dfrac{d'}{d}\right|=-\dfrac{d'}{d}=2\Leftrightarrow d'=-2d\)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};\left|\dfrac{d_1'}{d_1}\right|=3\Rightarrow-\dfrac{d_1'}{d_1}=3\Leftrightarrow d_1'=-3d_1\)
\(d_1+d_1'-d-d'=10\Leftrightarrow d_1-3d_1-d+2d=10\Leftrightarrow d-2d_1=10\left(1\right)\)
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{d_1}+\dfrac{1}{d_1'}\Leftrightarrow\dfrac{1}{d}-\dfrac{1}{2d}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\Leftrightarrow3d_1=4d\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}d=-6\\d_1=-8\end{matrix}\right.\) vô lý vì d và d1 phải dương, bạn xem lại đề bài, bởi ngay từ ban đầu bạn đã biết nằm trong khoảng từ f đến 2f thì ảnh cao hơn vật là đúng, nhưng ra khỏi 2f thì nó luôn thấp hơn chứ ko thể nào cao hơn được. Nếu khoảng cách lúc sau bé hơn 10cm so với lúc đầu thì mới đúng.


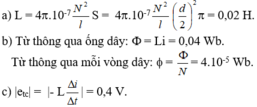

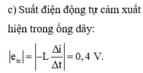
Bài 1:
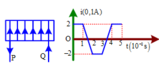
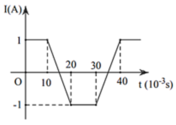
a/ \(i_1=0,8\left(5-t_1\right);i_2=0,8\left(5-t_2\right)\)
\(\Rightarrow\Delta i=i_2-i_1=0,8.5-0,8t_2-0,8.5+0,8t_1=0,8\left(t_1-t_2\right)\)
\(\Rightarrow\frac{\Delta i}{\Delta t}=\frac{0,8\left(t_1-t_2\right)}{-\left(t_1-t_2\right)}=-0,8\left(A/s\right)\)
b/ \(E_{tc}=L.\left|\frac{\Delta i}{\Delta t}\right|=0,005.\left|-0,8\right|=4.10^{-3}\left(V\right)\)
Bài 2:
a/ \(B_{1M}=2.10^{-7}.\frac{I_1}{r_1}=2.10^{-7}.\frac{5}{0,05}=2.10^{-5}\left(T\right)\)
b/ \(B_{2M}=2.10^{-7}.\frac{I_2}{r_2}=2.10^{-7}.\frac{10}{0,05}=4.10^{-5}\left(T\right)\)
\(\overrightarrow{I_1}\uparrow\downarrow\overrightarrow{I_2}\Rightarrow\overrightarrow{B_{1M}}\uparrow\downarrow\overrightarrow{B_{2M}}\Rightarrow\sum B=\left|B_{1M}-B_{2M}\right|=\left|2.10^{-5}-4.10^{-5}\right|=2.10^{-5}\left(T\right)\)
\(\sum B=0\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{B_{1M}}\uparrow\downarrow\overrightarrow{B_{2M}}\\B_{1M}=B_{2M}\end{matrix}\right.\Leftrightarrow\frac{I_1}{r_1}=\frac{I_2}{r_2}\Leftrightarrow\frac{5}{r_1}=\frac{10}{r_2}\)
Theo câu trên ta có: \(r_1+r_2=10\left(cm\right)\Rightarrow\left\{{}\begin{matrix}r_2=2r_1\\r_1+r_2=0,1\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}r_1=\frac{1}{30}\left(m\right)\\r_2=\frac{1}{15}\left(m\right)\end{matrix}\right.\)
hiện giờ mình làm lạc mất hình vẽ của bài 3 rồi nên chắc bài này không giải được nữa, cảm ơn bạn nhiều :)))