Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: C
HD Giải:
Theo tính thuận nghich của đường truyền sáng ta có:
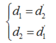
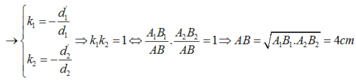
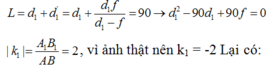
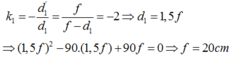

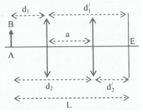
+ Theo tính thuận nghịch của chiều truyền ánh sáng 
@ Ta có thể giải cách khác như sau:
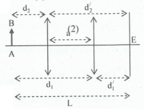

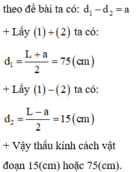


b) Để có 1 vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải có nghiệm kép nên:
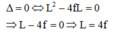
c) Để không có vị trí của thấu kính cho ảnh rõ nét trên màn thì phương trình (*) phải vô nghiệm nên:
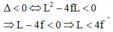


a) Chứng minh:
\(d+d' =a \Rightarrow d' = a -d\)
Và \(f=\frac{d.d'}{d+d'} \Rightarrow d = \frac{d.(a-d)}{a}\)
\( \Rightarrow d^2 -ad + af =0\)
\( \Delta = a^2 -4af =a(a-4f)\)
(Điều kiện để phương trình có nghiệm là \(a \geq 4f \))
Vì đã có 1 ảnh rõ nét rồi nên phương trình sẽ có nghiệm, vì có vị trí thứ 2 nữa nên phương trình phải có 2 nghiệm phân biệt.
Ta có hai vị trí này là 2 nghiệm có phương trình:
\( d_1 = \frac{a+ \sqrt{\Delta}}{2}\)
\(d_2 = \frac{a- \sqrt{\Delta}}{2}\)
b) Gọi l =khoảng cách 2 vị trí trên ta có:
\( l = d_2 -d_1 = \frac{a+ \sqrt { \Delta} - (a- \sqrt { \Delta})}{2} = \sqrt{\Delta} \)
Ta có: \(l^2 = \Delta = a^2 -4af \Rightarrow f = \frac{a^2 -l^2 }{4a}\)
Để đo tiêu cự chỉ cần đo khoảng cách giữa 2 vị trị cho ảnh rõ nét trên màn và khoảng cách giữa vật- màn. Phương pháp này gọi là phương pháp Bessel. Hoặc có thể dùng bất đẳng thức Cauchy để chứng minh cũng được nhé!

Đáp án: C
HD Giải:
Theo tính thuận nghich của đường truyền sáng ta có
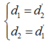
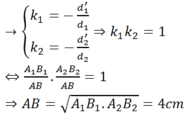

Chọn đáp án D.
Theo bài ra ta có: d + d’ = L nên d’ = L – d
Mặt khác:
1 f = 1 d + 1 d ' ⇔ 1 f = 1 d + 1 L − d ⇔ d L − d = L f ⇔ d 2 − L d + L f = 0 (*)
Vì chỉ có một vị trí duy nhất của thấu kính tại đó có ảnh của vật hiện lên rõ nét trên màn nên phương trình (*) có nghiệm duy nhất ⇔ Δ = L 2 − 4 L f = 0 ⇔ f = L 4 = 5 c m .

Sơ đồ tạo ảnh:

Khoảng cách giữa vật và ảnh qua thấu kính L = |d + d'|
Vì vật thật, ảnh thật nên L = d + d'
Theo giả thiết có hai vị trí cho ảnh rõ nét trên màn. Gọi hai vị trí vật và ảnh tương ứng là

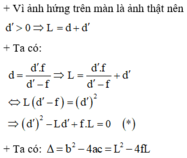

Bài 1:
a/ \(L=4\pi^2.10^{-7}.\dfrac{N^2}{l}S=4\pi^2.10^{-7}.\dfrac{1000^2}{0,3}.0,04^2.\pi=...\left(H\right)\)
b/ \(\phi=L.i=...\left(Wb\right)\)
c/ \(\xi=\dfrac{L.\Delta i}{\Delta t}=\dfrac{L.\left(2-0\right)}{0,1}=...\left(V\right)\)
2/
a/ \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\Leftrightarrow10=\dfrac{1}{0,3}+\dfrac{1}{d'}\Leftrightarrow d'=15\left(cm\right)\)
\(h'=\left|\dfrac{d'}{d}\right|.h=\left|\dfrac{15}{30}\right|.2=1\left(cm\right)\)
b/ Chắc là màn cố định nhỉ?
\(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'};\left|\dfrac{d'}{d}\right|=2\)
Vì cho ảnh rõ nét trên màn nên ảnh là ảnh thật và ngược chiều với vật
\(\Rightarrow\left|\dfrac{d'}{d}\right|=-\dfrac{d'}{d}=2\Leftrightarrow d'=-2d\)
\(\dfrac{1}{f}=\dfrac{1}{d_1}+\dfrac{1}{d_1'};\left|\dfrac{d_1'}{d_1}\right|=3\Rightarrow-\dfrac{d_1'}{d_1}=3\Leftrightarrow d_1'=-3d_1\)
\(d_1+d_1'-d-d'=10\Leftrightarrow d_1-3d_1-d+2d=10\Leftrightarrow d-2d_1=10\left(1\right)\)
\(\dfrac{1}{d}+\dfrac{1}{d'}=\dfrac{1}{d_1}+\dfrac{1}{d_1'}\Leftrightarrow\dfrac{1}{d}-\dfrac{1}{2d}=\dfrac{1}{d_1}-\dfrac{1}{3d_1}\Leftrightarrow3d_1=4d\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\left\{{}\begin{matrix}d=-6\\d_1=-8\end{matrix}\right.\) vô lý vì d và d1 phải dương, bạn xem lại đề bài, bởi ngay từ ban đầu bạn đã biết nằm trong khoảng từ f đến 2f thì ảnh cao hơn vật là đúng, nhưng ra khỏi 2f thì nó luôn thấp hơn chứ ko thể nào cao hơn được. Nếu khoảng cách lúc sau bé hơn 10cm so với lúc đầu thì mới đúng.