Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
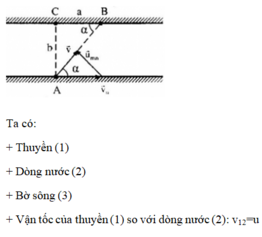
Theo đề ta có:
\(v_{23}=v^0\)
\(v_{13}=\sqrt{a^2+b^2}\)
\(\Leftrightarrow v_{13}=v_{12}+v_{23}\)
\(\Rightarrow v_{12}=\sqrt{a^2+b^2}-v^0\)
Vì \(v^0\) không đổi
Để \(v_{12}\) min thì \(\sqrt{a^2+b^2}\) min
\(\Leftrightarrow \) \(a^2+b^2\) min
Mà \(a^2+b^2\) \(\geq 2\) \(\sqrt{ab}\)
Dấu ''='' xảy ra khi
\(a=b\)
Vậy: \(v_{12}=a\sqrt{2}-v^0\)
\(\Leftrightarrow \)

Chọn C.
Gọi người bơi là (1), dòng nước là (2)
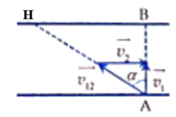
Để bơi sang sông với quãng đường ngắn nhất người đó phải bơi sao cho vận tốc v 12 ⇀ (vận tốc của người đối với nước) có hướng như hình vẽ để v 10 ⇀ (vận tốc của người đối với bờ sông) có phương vuông góc với bờ sông và thoả mãn:
v 10 ⇀ = v 20 ⇀ + v 12 ⇀
( v 20 ⇀ là vận tốc dòng chảy của nước)
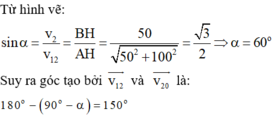



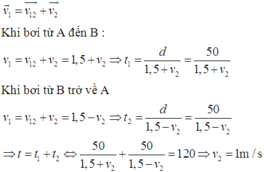
Bài này nên dùng đạo hàm :3
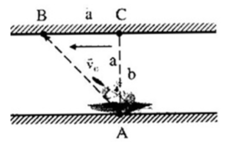
Thời gian để ng đó bơi thẳng đến B là
\(t=\frac{d}{v_2}\left(h\right)\)
Thời gian để ng đó chay 1 quãng là a-x r bơi đến B là (x là khoảng cách từ nơi mà ng chạy đến rồi nhảy đến hình chiếu của B hạ xuống mp)
\(t=\frac{a-x}{v_1}+\frac{\sqrt{x^2+d^2}}{v_2}\)
\(t'=\frac{-1}{v_1}+\frac{1}{v_2}.\frac{x}{\sqrt{x^2+h^2}}=0\)
\(\Leftrightarrow v_1x=v_2\sqrt{x^2+d^2}\)
\(\Leftrightarrow v_1^2x^2=v_2^2\left(x^2+d^2\right)\)
\(\Leftrightarrow x=\frac{v_2d}{\sqrt{v_1^2-v_2^2}}\)
=> t=...
bạn tự thay vào r so sánh:3
C là gì vậy ạ