Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài này nên dùng đạo hàm :3
Thời gian để ng đó bơi thẳng đến B là
\(t=\frac{d}{v_2}\left(h\right)\)
Thời gian để ng đó chay 1 quãng là a-x r bơi đến B là (x là khoảng cách từ nơi mà ng chạy đến rồi nhảy đến hình chiếu của B hạ xuống mp)
\(t=\frac{a-x}{v_1}+\frac{\sqrt{x^2+d^2}}{v_2}\)
\(t'=\frac{-1}{v_1}+\frac{1}{v_2}.\frac{x}{\sqrt{x^2+h^2}}=0\)
\(\Leftrightarrow v_1x=v_2\sqrt{x^2+d^2}\)
\(\Leftrightarrow v_1^2x^2=v_2^2\left(x^2+d^2\right)\)
\(\Leftrightarrow x=\frac{v_2d}{\sqrt{v_1^2-v_2^2}}\)
=> t=...
bạn tự thay vào r so sánh:3

Chọn C.
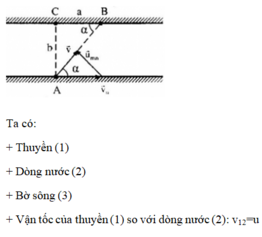
Gọi người bơi là (1), dòng nước là (2)
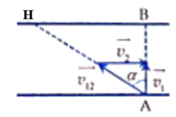
Để bơi sang sông với quãng đường ngắn nhất người đó phải bơi sao cho vận tốc v 12 ⇀ (vận tốc của người đối với nước) có hướng như hình vẽ để v 10 ⇀ (vận tốc của người đối với bờ sông) có phương vuông góc với bờ sông và thoả mãn:
v 10 ⇀ = v 20 ⇀ + v 12 ⇀
( v 20 ⇀ là vận tốc dòng chảy của nước)
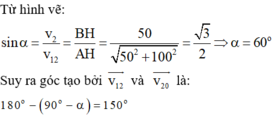

Đáp án B
Gọi người là (1), dòng nước là (2)
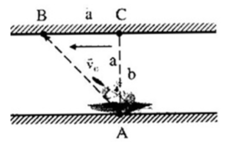
Khi bơi theo hướng vuông góc với dòng chảy (hình a), khi đó người bơi đến điểm B, cách H một khoảng 50m
⇒ v 2 v 12 = 1 2
Để điểm B trùng với điểm H, hướng bơi ngoài đó (so với nước) có v 12 → phải như hình b
⇒ sin α = v 2 v 12 . Lưu ý : v 2 = v
Vậy sin α = 1 2 ⇒ α = 60 0
Nghĩa là người đó phải bơi theo hướng tạo với dòng chảy (tạo với v 2 → ) một góc bằng 1200

Chọn C.
Gọi người bơi là (1), dòng nước là (2)
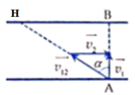
Để bơi sang sông với quãng đường ngắn nhất người đó phải bơi sao cho vận tốc v 12 → (vận tốc của người đối với nước) có hướng như hình vẽ để v 10 → (vận tốc của người đối với bờ sông) có phương vuông góc với bờ sông và thoả mãn:
v 10 → = v 12 → + v 20 →
( v 20 → là vận tốc dòng chảy của nước)
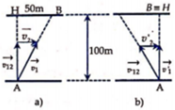
Từ hình vẽ:
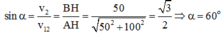
Suy ra góc tạo bởi v 12 → và v 20 → là:
![]()

Đáp án A
Gọi d là độ rộng của dòng sông. Từ kết quả của các bài trước suy ra tổng thời gian bơi của người thứ nhất là:
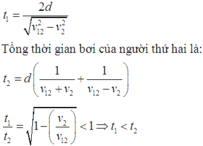



bơi thẳng từ A đến B