Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trên tia đối của tia BA lấy I sao cho BI = DQ
\(\Delta DCQ=\Delta BCI\left(c.g.c\right)\Rightarrow\hept{\begin{cases}CQ=CI\\\widehat{DCQ}=\widehat{BCI}\end{cases}}\)
Ta có: \(\widehat{QCI}=\widehat{QCB}+\widehat{BCI}=\widehat{QCB}+\widehat{DCQ}=\widehat{BCD}=90^0\)
Ta có: \(AP+AQ+PQ=2AB\)
\(\Rightarrow AP+AQ+PQ=AP+PB+AQ+QD\)
\(\Rightarrow PQ=PB+QD\)
\(\Rightarrow PQ=PB+BI\Rightarrow PQ=PI\)
\(\Delta PCQ=\Delta PCI\left(c.c.c\right)\Rightarrow\widehat{PCQ}=\widehat{PCI}=\frac{\widehat{QCI}}{2}=\frac{90^0}{2}=45^0\)

1.
Tam giác AMC vuông tại M với đường cao MD
Áp dụng hệ thức lượng: \(AM^2=AD.AC\) (1)
Tương tự ta có:
\(AN^2=AE.AB\) (2)
Mặt khác xét hai tam giác vuông ABD và ACE có:
\(\widehat{BAC}\) chung
\(\Rightarrow\Delta_VABD\sim\Delta_VACE\) (g.g)
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Leftrightarrow AB.AE=AC.AD\) (3)
(1);(2);(3) \(\Rightarrow AM^2=AN^2\) \(\Rightarrow AM=AN\)
Bài 2 tham khảo tại đây:
Cho tam giác ABC vuông tại A , đường cao AH . Biết AB/AC = 20/21 , AH = 420 . Tính chu vi tam giác ABC - Hoc24

Theo đề có: `ΔAMC` là Δ vuông, đường cao `MD`.
=> `AM^2=AD.AC` (1)
`ΔANB` là Δ vuông, đường cao `NE`:
=> `AN^2=AE.AB` (2)
Lại có: `ΔABD=ΔACE`(g.g)
=> \(\dfrac{AB}{AC}=\dfrac{AD}{AE}\Leftrightarrow AB.AE=AC.AD\left(3\right)\)
Từ (1), (2), (3) suy ra: `AM=AD` (đpcm)
$HaNa$

Xét ΔADB vuông tạiD và ΔAEC vuông tại E có
góc DAB chung
DO đó: ΔADB\(\sim\)ΔAEC
Suy ra: AD/AE=AB/AC
hay \(AD\cdot AC=AB\cdot AE\left(1\right)\)
Xét ΔAMC vuông tại M có MD là đường cao
nên \(AD\cdot AC=AM^2\left(2\right)\)
Xét ΔANB vuông tại N có NE là đường cao
nên \(AE\cdot AB=AN^2\left(3\right)\)
Từ (1), (2) và (3) suy ra AM=AN
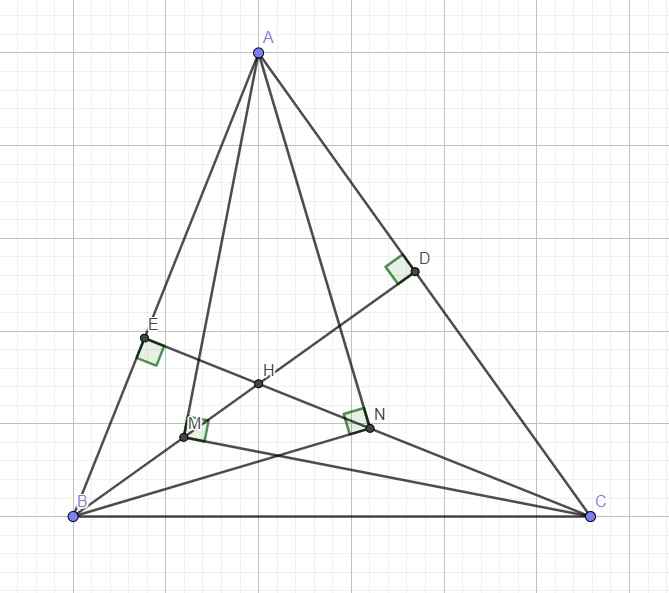
1.
Xét tam giác $ABD$ và $ACE$ có:
\(\left\{\begin{matrix} \widehat{A}-\text{chung}\\ \widehat{ADB}=\widehat{AEC}=90^0\end{matrix}\right.\Rightarrow \triangle ABD\sim \triangle ACE(g.g)\)
\(\Rightarrow \frac{AB}{AC}=\frac{AD}{AE}\Rightarrow AE.AB=AC.AD(1)\)
Xét tam giác $ADM$ và $AMC$ có:
\(\left\{\begin{matrix} \text{A}-\text{chung}\\ \widehat{ADM}=\widehat{AMC}(=90^0)\end{matrix}\right.\Rightarrow \triangle ADM\sim \triangle AMC(g.g)\)
\(\Rightarrow \frac{AD}{AM}=\frac{AM}{AC}\Rightarrow AM^2=AD.AC(2)\)
Xét tam giác $AEN$ và $ANB$ có:
\(\left\{\begin{matrix} \widehat{A}-\text{chung}\\ \widehat{AEN}=\widehat{ANB}(=90^0)\end{matrix}\right.\Rightarrow \triangle AEN\sim \triangle ANB(g.g)\)
\(\Rightarrow \frac{AE}{AN}=\frac{AN}{AB}\Rightarrow AN^2=AE.AB(3)\)
Từ \((1);(2);(3)\Rightarrow AM^2=AN^2\Rightarrow AM=AN\) (đpcm)
Hình vẽ 1: