Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 4 :
a, Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AB^2=BH.BC=16\Rightarrow AB=4\)cm
Theo định lí Ptago : \(AC=\sqrt{BC^2-AB^2}=\sqrt{64-16}=4\sqrt{3}\)cm
* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{16\sqrt{3}}{8}=2\sqrt{3}\)cm
b, Xét tam giác ABK vuông tại A, đường cao AD
\(AB^2=BD.BK\)( hệ thức lượng ) (1)
Xét tam giác ABC vuông tại A, đường cao AH
\(AB^2=BH.BC\)( hệ thức lượng ) (2)
Từ (1) ; (2) => \(BD.BK=BH.BC\)(3)
c, Xét tam giác BHD và tam giác BKC
^B _ chung
(3) => \(BD.BK=BH.BC\Rightarrow\frac{BD}{BC}=\frac{BH}{BK}\)
Vậy tam giác BHD ~ tam giác BKC ( c.g.c )
=> \(\frac{S_{BHD}}{S_{BKC}}=\left(\frac{BD}{BC}\right)^2\)(4)
Ta có : cosABD = \(\frac{DB}{AB}\)
=> cos2ABD = \(\left(\frac{DB}{AB}\right)^2\)=> cos2ABD = \(\frac{DB^2}{AB^2}=\frac{DB^2}{16}\)
=> \(\frac{1}{4}cos^2\widehat{ABD}=\frac{DB^2}{64}=\frac{DB^2}{8^2}=\frac{DB^2}{BC^2}=\left(\frac{DB}{BC}\right)^2\)
\(\Rightarrow\frac{1}{4}cos^2\widehat{ABD}=\frac{S_{BHD}}{S_{BKC}}\)theo (4)
=> \(S_{BHD}=S_{BKC}.\frac{1}{4}cos^2\widehat{ABD}\)
Bài 3 :
a, Với \(x>0;x\ne1\)
\(A=\left(\frac{1}{x+2\sqrt{x}}-\frac{1}{\sqrt{x}+2}\right):\frac{1-\sqrt{x}}{x+4\sqrt{x}+4}\)
\(=\left(\frac{1-\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+2\right)}\right):\frac{1-\sqrt{x}}{\left(\sqrt{x}+2\right)^2}=\frac{\sqrt{x}+2}{\sqrt{x}}\)
b, Ta có : \(A=\frac{5}{3}\Rightarrow\frac{\sqrt{x}+2}{\sqrt{x}}=\frac{5}{3}\Rightarrow3\sqrt{x}+6=5\sqrt{x}\Leftrightarrow6=2\sqrt{x}\Leftrightarrow x=9\)

\(a,\sqrt{x-2}\)có nghĩa khi\(\sqrt{x-2}\ge0\)
\(\Rightarrow x\ge2\)
\(b,\frac{1}{\sqrt{2x-1}}\)có nghĩa khi \(\sqrt{2x-1}>0\)
\(\Rightarrow2x>1\)
\(\Rightarrow x>\frac{1}{2}\)


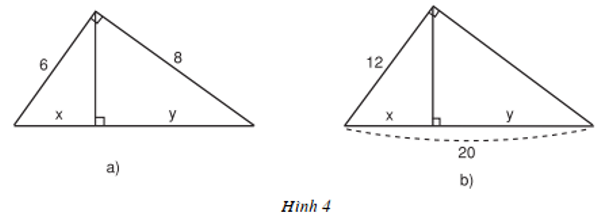
Hình a/
Áp dụng định lý Pitago:
$x+y=\sqrt{6^2+8^2}=10$
Áp dụng hệ thức lượng trong tam giác vuông:
$6^2=x(x+y)=10x\Rightarrow x=3,6$
$8^2=y(y+x)=10y\Rightarrow y=6,4$
Hình b/
Áp dụng hệ thức lượng trong tam giác vuông:
$12^2=x(x+y)=20x$
$\Rightarrow x=\frac{12^2}{20}=7,2$
$y=20-x=20-7,2=12,8$

:v Làm bài 31 thôi nhá , còn lại all tự làm -..-
Gọi x (cm) , y (cm) là độ dài hai cạnh góc vuông của tam giác vuông (x > 2, y > 4).
Diện tích tam giác ban đầu là \(\frac{1}{2}xy\left(cm^2\right)\)
+ Tăng mỗi cạnh lên 3cm thì tam giác vuông mới có độ dài 2 cạnh là x + 3(cm) và y + 3 (cm)
Diện tích tam giác mới là : \(\frac{1}{2}\left(x+3\right)\left(y+3\right)\left(cm^2\right)\)
Diện tích tăng thêm 36 cm2 nên ta có p/trình :
\(\frac{1}{2}\left(x+3\right)\left(y+3\right)=\frac{1}{2}xy+36\)
\(\Leftrightarrow\left(x+3\right)\left(y+3\right)=xy+72\)
\(\Leftrightarrow xy+3x+3y+9=xy+72\)
\(\Leftrightarrow3x+3y=63\)
\(\Leftrightarrow x+y=21\)
+ Giảm một cạnh 2cm và giảm cạnh kia 4cm thì tam giác vuông mới có 2 cạnh là : x – 2 (cm) và y – 4 (cm).
Diện tích tam giác mới là : \(\frac{1}{2}\left(x-2\right)\left(y-4\right)\left(cm^2\right)\)
Diện tích giảm đi 26cm2 nên ta có phương trình :
\(\frac{1}{2}\left(x-2\right)\left(y-4\right)=\frac{1}{2}xy-26\)
\(\Leftrightarrow\left(x-2\right)\left(y-4\right)=xy-52\)
\(\Leftrightarrow xy-4x-2y+8=xy-52\)
\(\Leftrightarrow4x+2y=60\)
\(\Leftrightarrow2x+y=30\)
Ta có hệ phương trình : \(\hept{\begin{cases}x+y=21\\2x+y=30\end{cases}}\)
Lấy phương trình thứ hai trừ phương trình thứ nhất ta được :
\(\hept{\begin{cases}\left(2x+y\right)-\left(x+y\right)=30-21\\x+y=21\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}2x+y-\left(x+y\right)=9\\x+y=21\end{cases}\Leftrightarrow\hept{\begin{cases}x=9\\y=12\end{cases}}}\)
Vậy tam giác có hai cạnh lần lượt là 9cm và 12cm

B A C a
a, Ta có : tan a = CB/AB
sin a / cos a = CB/AC / BA/AC = CB/AB
=> ĐPCM
Tương tự với cái kia nhaaaaaa
Do tan a = CB/AB (1)
Mà cot a = AB/CD (2)
Nhân theo vế (1) và (2) ta có ngay đpcm
b, Ta có : \(VT=\frac{AB^2}{AC^2}+\frac{BC^2}{AC^2}=\frac{AB^2+BC^2}{AC^2}=1\)(pitago)

Hàm số y=m−3.x+23 là hàm số bậc nhất khi hệ số của x là a=m−3≠0
Ta có: m−3≠0⇔m−3>0⇔m>3
Vậy khi m>3 thì hàm số y=m−3x+23 là hàm số bậc nhất
Câu b
S=1m+2t−34 (t là biến số).
Phương pháp giải:
Để hàm số được cho bởi công thức y=ax+b là hàm số bậc nhất thì a≠0 .
Lời giải chi tiết:
Hàm số S=1m+2t−34 là hàm số bậc nhất khi hệ số của t là a=1m+2≠0
Ta có: 1m+2≠0⇔m+2≠0⇔m≠−2
Vậy khi m≠−2 thì hàm số S=1m+2t−34 là hàm số bậc nhất.
Lời giải và đáp án
Đây là dạng toán hàm số bậc nhất nha bạn, áp dụng vào và làm là được!
\(a.\)\(\text{Hàm số }y=(\sqrt{m-3)}x+\frac{2}{3}\) \(\text{là hàm số bậc nhất khi hệ số của }\)\(x\)\(\text{là}\)\(a=\sqrt{m-3\ne}0\)
\(\text{Ta có: }\sqrt{m-3}m-3\ne0\Leftrightarrow m-3>0\Leftrightarrow m>3\)
\(\text{Vậy khi}\) \(m>3\)\(\text{thì hàm số }y=(\sqrt{m-3})x+\frac{2}{3}\text{ là hàm số bậc nhất.}\)
\(b.\) \(\text{Hàm số }S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất khi hệ số của }t\text{ là }a=:\frac{1}{m+2}\ne0\)
\(\text{Ta có: }\frac{1}{m+2}\ne0\Leftrightarrow m+2\ne0\Leftrightarrow m\ne-2\)
\(\text{Vậy khi}\) \(m\ne-2\text{thì hàm số}\)\(S=:\frac{1}{m+2}t-\frac{3}{4}\text{là hàm số bậc nhất.}\)

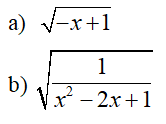
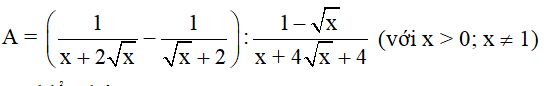
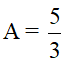
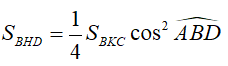
![[Năm 2021] Đề thi Giữa kì 1 Toán lớp 9 có đáp án (10 đề)](https://vietjack.com/de-kiem-tra-lop-9/images/de-thi-giua-ki-1-toan-lop-9-co-dap-an-2021-24855.png)
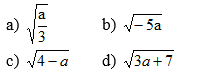
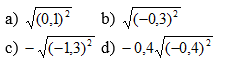
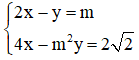

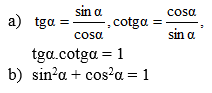
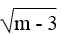 )x + 2/3
)x + 2/3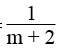 t - 3/4 (t là biến số)
t - 3/4 (t là biến số)
a)\(\sqrt{81}-\sqrt{80}\)\(.\sqrt{0,2}\)\(=\sqrt{9^2}-\sqrt{80.0,2}\)\(=9-\sqrt{16}\)\(=9-4=5\)
\(\sqrt{\left(2-\sqrt{5}\right)^2}\)\(-\frac{1}{2}.\sqrt{20}\)\(=|2-\sqrt{5}|-\frac{1}{2}.\sqrt{4.5}\)\(=2-\sqrt{5}-\frac{1}{2}.2\sqrt{5}\)
\(=2-\sqrt{5}-\sqrt{5}=2\)
Tôi lm đc đến đây thôi(@_@)
\(\)
ko biết