K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 10 2023
a: Ta có:
\(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\)
\(\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)=\dfrac{2}{5}+\dfrac{2}{5}=\dfrac{4}{5}\)
\(\dfrac{4}{5}=\dfrac{4}{5}\). Vậy \(\left(\dfrac{2}{5}+\dfrac{1}{5}\right)+\dfrac{1}{5}=\dfrac{2}{5}+\left(\dfrac{1}{5}+\dfrac{1}{5}\right)\)
Ta có:
\(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{7}{9}+\dfrac{1}{9}=\dfrac{8}{9}\)
\(\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)=\dfrac{2}{9}+\dfrac{6}{9}=\dfrac{8}{9}\)
\(\dfrac{8}{9}=\dfrac{8}{9}\). Vậy \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}=\dfrac{2}{9}+\left(\dfrac{5}{9}+\dfrac{1}{9}\right)\)
b: \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{3}{3}+\dfrac{4}{3}=\dfrac{7}{3}\)
\(\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)=\dfrac{1}{3}+\dfrac{6}{3}=\dfrac{7}{3}\)
\(\dfrac{7}{3}=\dfrac{7}{3}\). Vậy \(\left(\dfrac{1}{3}+\dfrac{2}{3}\right)+\dfrac{4}{3}=\dfrac{1}{3}+\left(\dfrac{2}{3}+\dfrac{4}{3}\right)\)
29 tháng 10 2023
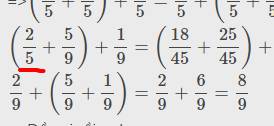
Đề của anh bị sai mới đúng chứ ạ? Anh Đạt ghi là \(\left(\dfrac{2}{9}+\dfrac{5}{9}\right)+\dfrac{1}{9}\) chứ có phải \(\dfrac{2}{5}\) đâu ạ?
BQ
1
13 tháng 5 2017
\(1-\left(\frac{12}{5}+y=\frac{8}{9}\right):\frac{16}{9}=0\)
\(1-\left(\frac{12}{5}+y-\frac{8}{9}\right)=0\times\frac{16}{9}\)
\(1-\left(\frac{12}{5}+y-\frac{8}{9}\right)=0\)
\(\frac{12}{5}+y-\frac{8}{9}=1-0\)
\(\frac{12}{5}-y+\frac{8}{9}=1\)
\(\frac{12}{5}-y=1-\frac{8}{9}\)
\(\frac{12}{5}-y=\frac{1}{9}\)
\(y=\frac{12}{5}-\frac{1}{9}\)
\(y=\frac{108}{45}-\frac{5}{45}\)
\(y=\frac{103}{45}\)
HQ
Hà Quang Minh
Giáo viên
27 tháng 11 2023
a) $\frac{{14}}{{18}}:\frac{8}{9} = \frac{7}{9}:\frac{8}{9} = \frac{7}{9} \times \frac{9}{8} = \frac{{63}}{{72}} = \frac{7}{8}$
b) $\frac{9}{6}:\frac{3}{{10}} = \frac{3}{2}:\frac{3}{{10}} = \frac{3}{2} \times \frac{{10}}{3} = \frac{{30}}{6} = 5$
c) $\frac{4}{5}:\frac{{10}}{{15}} = \frac{4}{5}:\frac{2}{3} = \frac{4}{5} \times \frac{3}{2} = \frac{{12}}{{10}} = \frac{6}{5}$
d) $\frac{1}{6}:\frac{{21}}{9} = \frac{1}{6}:\frac{7}{3} = \frac{1}{6} \times \frac{3}{7} = \frac{3}{{42}} = \frac{1}{{14}}$
C
6 tháng 3 2023
\(\dfrac{3}{5}+\dfrac{1}{2}+\dfrac{8}{15}\\ =\dfrac{3\times6}{5\times6}+\dfrac{1\times15}{2\times15}+\dfrac{8\times2}{15\times2}\\ =\dfrac{18}{30}+\dfrac{15}{30}+\dfrac{16}{30}\\ =\dfrac{49}{30}\\ \dfrac{6}{9}+\dfrac{14}{18}-\dfrac{5}{6}\\ =\dfrac{6\times2}{9\times2}+\dfrac{14}{18}-\dfrac{5\times3}{6\times3}\\ =\dfrac{12}{18}+\dfrac{14}{18}-\dfrac{15}{18}\\ =\dfrac{11}{18}\)
\(\dfrac{9}{20}-\dfrac{3}{5}:\dfrac{4}{1}\\ =\dfrac{9}{20}-\dfrac{3}{5}\times\dfrac{1}{4}\\ =\dfrac{9}{20}-\dfrac{3}{20}\\ =\dfrac{6}{20}\\ =\dfrac{3}{10}\)
\(\dfrac{1}{6}+\dfrac{2}{3}\times\dfrac{8}{9}\\=\dfrac{1}{6}+\dfrac{16}{27}\\ =\dfrac{1\times9}{6\times9}+\dfrac{16\times2}{27\times2}\\ =\dfrac{9}{54}+\dfrac{32}{54}\\ =\dfrac{41}{54}.\)
24 tháng 2 2022
a, \(=\dfrac{1+4}{5}+\dfrac{5+1+3}{9}=1+1=2\)
b, \(=\dfrac{1+4+2}{3}+\dfrac{1+2+5}{6}=\dfrac{6}{3}+\dfrac{8}{6}=2+\dfrac{4}{3}=\dfrac{6+4}{3}=\dfrac{10}{3}\)
29 tháng 10 2023
a: \(\dfrac{3}{8}+\dfrac{7}{8}=\dfrac{3+7}{8}=\dfrac{10}{8}=\dfrac{5}{4}\)
b: \(\dfrac{7}{9}-\dfrac{4}{9}=\dfrac{7-4}{9}=\dfrac{3}{9}=\dfrac{1}{3}\)
c: \(\dfrac{5}{6}+\dfrac{1}{8}=\dfrac{20}{24}+\dfrac{3}{24}=\dfrac{20+3}{24}=\dfrac{23}{24}\)
d: \(\dfrac{9}{15}-\dfrac{2}{5}=\dfrac{3}{5}-\dfrac{2}{5}=\dfrac{3-2}{5}=\dfrac{1}{5}\)
e: \(\dfrac{2}{5}+\dfrac{3}{5}+\dfrac{9}{5}=\dfrac{2+3+9}{5}=\dfrac{14}{5}\)
g: \(\dfrac{8}{10}-\dfrac{1}{10}-\dfrac{3}{10}=\dfrac{8-1-3}{10}=\dfrac{4}{10}=\dfrac{2}{5}\)
h: \(\dfrac{23}{7}-\dfrac{4}{7}+\dfrac{2}{7}=\dfrac{23-4+2}{7}=\dfrac{21}{7}=3\)
NH
3 tháng 3 2023
a)
`2/3+5/2-3/4`
`=10/4-3/4+2/3`
`=7/4+2/3`
`=21/12+8/12`
`=29/12`
b)
`2/5xx1/2:1/3`
`=2/10xx3/1`
`=6/10=3/5`
c)
`2/9:2/9xx1/3`
`=2/9xx9/2xx1/3`
`=1xx1/3`
`=1/3`
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
3 tháng 3 2023
a, \(\dfrac{2}{3}\) + \(\dfrac{5}{2}\) - \(\dfrac{3}{4}\)
= \(\dfrac{8}{12}\) + \(\dfrac{30}{12}\) - \(\dfrac{9}{12}\)
= \(\dfrac{38-9}{12}\)
= \(\dfrac{29}{12}\)
b, \(\dfrac{2}{5}\) x \(\dfrac{1}{2}\) : \(\dfrac{1}{3}\)
= \(\dfrac{1}{5}\) x \(\dfrac{3}{1}\)
= \(\dfrac{3}{5}\)
c, \(\dfrac{2}{9}\) : \(\dfrac{2}{9}\) x \(\dfrac{1}{3}\)
= 1 x \(\dfrac{1}{3}\)
= \(\dfrac{1}{3}\)
8 tháng 7 2023
a: =4/5+1/5+2/3+1/3=1+1=2
b: =17/12+7/12+29/7-8/7=3+2=5
c: =3/5+2/5+16/7-1/7-1/7
=1+2=3
d: =2/5+3/5+2/3+1/3+7/4+1/4
=1+1+2
=4
`9:2/3-1/5`
`=9xx3/2-1/5`
`=27/2-1/5`
`=135/10-2/10`
`=133/10`
\(9\div\dfrac{2}{3}-\dfrac{1}{5}\)
\(=9\times\dfrac{3}{2}-\dfrac{1}{5}\)
\(=\dfrac{27}{2}-\dfrac{1}{5}\)
\(=\dfrac{135}{10}-\dfrac{2}{10}\)
\(=\dfrac{133}{10}\)