Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a )
ĐKXĐ : \(y\ne0\) , \(y\ne-1\)
\(P=\left(\dfrac{2y^2+1}{y^3+1}-\dfrac{y}{y+y^2}\right):\left(1-\dfrac{y^2-2y-1}{y^2-y+1}\right)\)
\(=\left(\dfrac{2y^2+1}{\left(y+1\right)\left(y^2-y+1\right)}-\dfrac{1}{y+1}\right):\left(\dfrac{y^2-y+1-y^2+2y+1}{y^2-y+1}\right)\)
\(=\dfrac{2y^2+1-y^2+y-1}{\left(y+1\right)\left(y^2-y+1\right)}:\dfrac{y+2}{y^2-y+1}\)
\(=\dfrac{y\left(y+1\right)}{\left(y+1\right)\left(y^2-y+1\right)}\times\dfrac{y^2-y+1}{y+2}\)
\(=\dfrac{y}{y+2}\)
Câu b :
\(\left|2y+5\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}2y+5=3\\-2y-5=3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}y=-1\\y=-4\end{matrix}\right.\)
Thay \(y=-1\) vào P ta được : \(P=\dfrac{-1}{-1+2}=-1\)
Thay \(y=-4\) vào P ta được : \(P=\dfrac{-4}{-4+2}=2\)
Câu c :
T chỉ biết lập luận thôi :
Để P chia hết cho 4 thì \(\dfrac{y}{y+2}\) chia hết cho 4 hay \(\dfrac{y}{y+2}\) phải là bội của 4.
Do \(y< y+2\) nên \(\dfrac{y}{y+2}\) không thể là các số 4 ; 8 ;12 ;.........
Nên \(\dfrac{y}{y+2}=0\) thì sẽ chia hết cho 4 . \(\Leftrightarrow y=0\) ( Loại )
Nên không có giá trị y nào hết .
Câu d :
\(P=3-m>2\)
\(\Leftrightarrow-m>-1\)
\(\Leftrightarrow m< 1\)

\(A=\dfrac{x^2-y^2+2y^2}{y\left(x-y\right)}\cdot\dfrac{-\left(x-y\right)}{x^2+y^2}+\dfrac{2x^2+2-2x^2+x}{2\left(2x-1\right)}\cdot\dfrac{-\left(2x-1\right)}{x+2}\)
\(=\dfrac{-1}{y}+\dfrac{-1}{2}=\dfrac{-2-y}{2y}\)

a: \(M=\dfrac{-y+4}{y-2}+\dfrac{1}{y-2}+\dfrac{3}{y+2}\)
\(=\dfrac{-y+5}{y-2}+\dfrac{3}{y+2}=\dfrac{-y^2-2y+5y+10+3y-6}{\left(y-2\right)\left(y+2\right)}\)
\(=\dfrac{-y^2+6y+4}{\left(y-2\right)\left(y+2\right)}\)
b: Khi y=3 thì \(M=\dfrac{-3^2+6\cdot3+4}{\left(3-2\right)\left(3+2\right)}=\dfrac{-5+18}{5}=\dfrac{13}{5}\)

a: ĐKXĐ: \(x,y\in R\)
b: \(A=\dfrac{\dfrac{1}{4}x^2+x^2y+\dfrac{1}{4}y+y^2+x^2y^2+\dfrac{1}{4}+\dfrac{3}{4}y}{x^2y^2+1+x^2-x^2y-y+y^2}\)
\(=\dfrac{\dfrac{1}{4}x^2+x^2y+x^2y^2+y+\dfrac{1}{4}+y^2}{x^2y^2+x^2+1+y^2-x^2y-y}\)
\(=\dfrac{\dfrac{1}{4}\left(x^2+1\right)+y\left(x^2+1\right)+x^2y^2+y^2}{\left(y^2+1\right)\left(x^2+1\right)-y\left(x^2+1\right)}\)
\(=\dfrac{\left(x^2+1\right)\left(y+\dfrac{1}{4}\right)+x^2y^2+y^2}{\left(x^2+1\right)\left(y^2-y+1\right)}\)
\(=\dfrac{\left(x^2+1\right)\left(y+\dfrac{1}{4}\right)+y^2\left(x^2+1\right)}{\left(x^2+1\right)\left(y^2-y+1\right)}=\dfrac{y^2+y+\dfrac{1}{4}}{y^2-y+1}\)

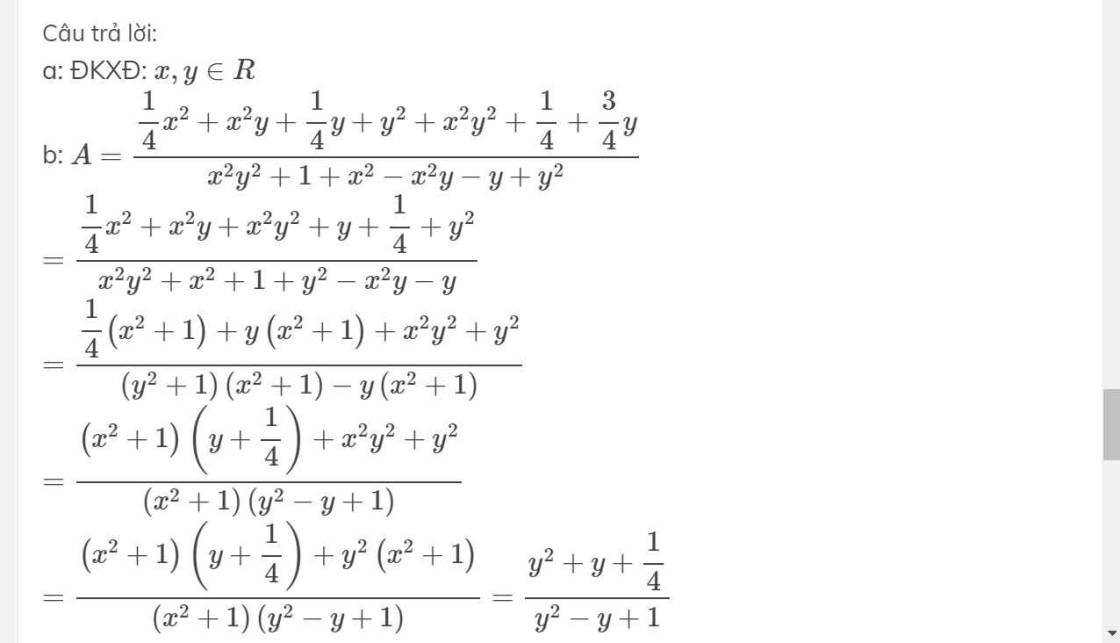
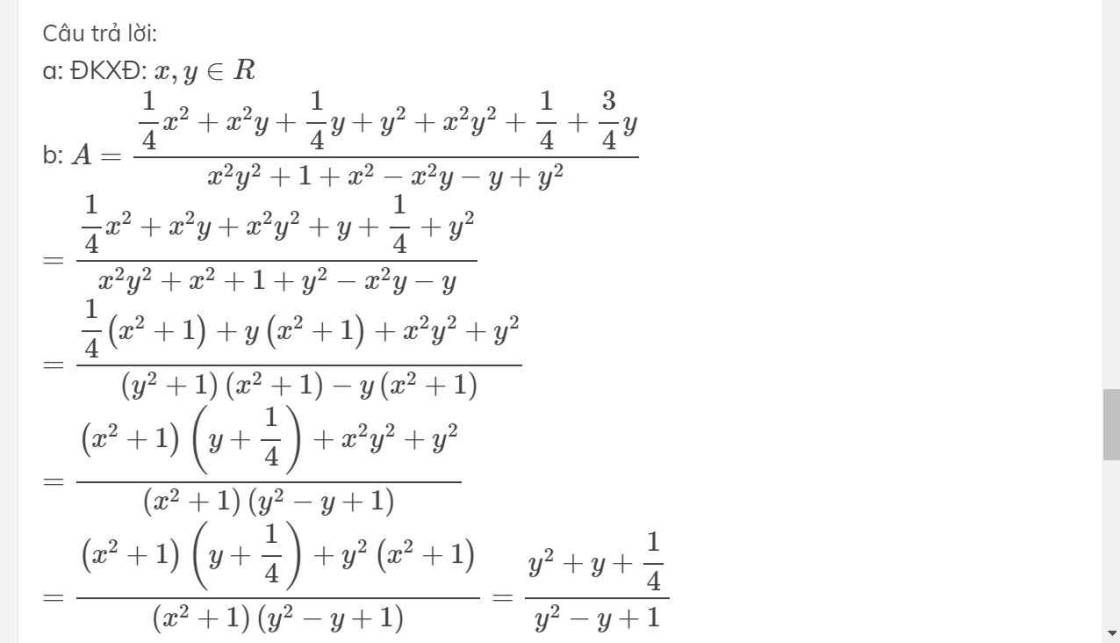
a: \(P=\left(\dfrac{2y^2+1}{\left(y+1\right)\left(y^2-y+1\right)}-\dfrac{1}{y+1}\right):\dfrac{y^2-y+1-y^2+2y+1}{y^2-y+1}\)
\(=\dfrac{2y^2+1-y^2+y-1}{\left(y+1\right)\left(y^2-y+1\right)}\cdot\dfrac{y^2-y+1}{y+2}\)
\(=\dfrac{y^2+y}{\left(y+1\right)}\cdot\dfrac{1}{y+2}=\dfrac{y}{y+2}\)
b: |2y+5|=3
=>2y+5=3 hoặc 2y+5=-3
=>2y=-2 hoặc 2y=-8
=>y=-1(loại) hoặc y=-4(nhận)
Thay y=-4 vào P,ta được:
\(P=\dfrac{-4}{-4+2}=\dfrac{-4}{-2}=2\)
c: Để P chia hết cho 4 thì P=4k
=>y=4k(y+2)