Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AJ}=\frac{3}{2}\overrightarrow{AM}=\frac{3}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)=\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{JK}=\overrightarrow{JA}+\overrightarrow{AK}=-\overrightarrow{AJ}+\overrightarrow{AK}=-\frac{3}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{AC}\)
\(=-\frac{3}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}\Rightarrow\left\{{}\begin{matrix}m=-\frac{3}{4}\\n=-\frac{1}{2}\end{matrix}\right.\)

Nối A vs N
a)xét tg CEF có: N là t/đ của EF(gt) và A là t/đ của FC (vì C đx vs F qua A) => AN là đg trung bình của tg CEF
=> AN//CE và AN =1/2. CE
=> AN=1/2.BC(vì BC = CE) => AN =BM(vì BM = 1/2. BC)
xét tg ANMB có: AN=MB (cmt) và AN//MB ( vì AN// CE ; B,M,C,E thẳng hàng) => tg ANMB là hbh=> MN//AB và AB=MN (1) ;
xét tg AGD có: I là t/đ của AG (gt) và K là t/đ của DG(gt) => IK là đg trung bình của tg AGD => IK=1/2.AD và IK //AD
Mà B là t/đ của AD (vì A đx vs D qua B) => AB=BD=1/2.AD=> IK=AB ( =1/2.AD) (2)
Từ (1),(2)=> IK=MN
Ta có: MN// AB(cmt) ; B thuộc AD => MN//AD
Xét tg MNIK có: IK=MN (cmt) và IK//MN (cùng // AD)
=> tg MNIK là hbh (đpcm)
b) Do tg MNIK là hbh ( câu a) mà G là gđ của IM và KN nên G là t/đ của IM là KN
=> IG=MG và KG=NG
Mặt khác: I là t/đ của AG(gt)=> IG=AI=> AI=IG=GM
K là t/đ của DG(gt) => Dk=KG => DK=KG=GN
xét tg ABC có: AM là đg trung tuyến (gt) và AI=IG=GM (cmt) => G là trọng tâm của tg ABC (*)
xét tg DEF có: DN là đg trung tuyến (gt) và DK=KG=GN(cmt) => G là trọng tâm của tg DEF (**)
Từ (*),(**) => G vừa là trọng tam của tg ABC vừa là trọng tâm của tg DEF
=> Tg ABC và tg DEF có cùng trọng tâm là G (đpcm)
Nối A vs N
a)xét tg CEF có: N là t/đ của EF(gt) và A là t/đ của FC (vì C đx vs F qua A) => AN là đg trung bình của tg CEF
=> AN//CE và AN =1/2. CE
=> AN=1/2.BC(vì BC = CE) => AN =BM(vì BM = 1/2. BC)
xét tg ANMB có: AN=MB (cmt) và AN//MB ( vì AN// CE ; B,M,C,E thẳng hàng) => tg ANMB là hbh=> MN//AB và AB=MN (1) ;
xét tg AGD có: I là t/đ của AG (gt) và K là t/đ của DG(gt) => IK là đg trung bình của tg AGD => IK=1/2.AD và IK //AD
Mà B là t/đ của AD (vì A đx vs D qua B) => AB=BD=1/2.AD=> IK=AB ( =1/2.AD) (2)
Từ (1),(2)=> IK=MN
Ta có: MN// AB(cmt) ; B thuộc AD => MN//AD
Xét tg MNIK có: IK=MN (cmt) và IK//MN (cùng // AD)
=> tg MNIK là hbh (đpcm)
b) Do tg MNIK là hbh ( câu a) mà G là gđ của IM và KN nên G là t/đ của IM là KN
=> IG=MG và KG=NG
Mặt khác: I là t/đ của AG(gt)=> IG=AI=> AI=IG=GM
K là t/đ của DG(gt) => Dk=KG => DK=KG=GN
xét tg ABC có: AM là đg trung tuyến (gt) và AI=IG=GM (cmt) => G là trọng tâm của tg ABC (*)
xét tg DEF có: DN là đg trung tuyến (gt) và DK=KG=GN(cmt) => G là trọng tâm của tg DEF (**)
Từ (*),(**) => G vừa là trọng tam của tg ABC vừa là trọng tâm của tg DEF
=> Tg ABC và tg DEF có cùng trọng tâm là G (đpcm)

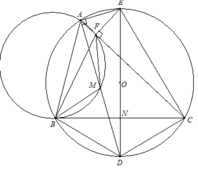
2). Từ AD là phân giác B A C ^ suy ra DB=DC vậy DE vuông góc với BC tại trung điểm N của BC.
Từ 1). Δ B D M ∽ Δ B C F , ta có D M C F = B D B C .
Vậy ta có biến đổi sau D A C F = 2 D M C F = 2 B D B C = C D C N = D E C E (3).
Ta lại có góc nội tiếp A D E ^ = F C E ^ (4).
Từ 3 và 4, suy ra Δ E A D ∽ Δ E F C ⇒ E F C ^ = E A D ^ = 90 ° ⇒ E F ⊥ A C

a: M(4;0) là trung điểm của AB
=>\(\left\{{}\begin{matrix}x_A+x_B=2\cdot4=8\\y_A+y_B=2\cdot0=0\end{matrix}\right.\)
N(5;2) là trung điểm của AC
=>\(\left\{{}\begin{matrix}x_A+x_C=2\cdot5=10\\y_A+y_C=2\cdot2=4\end{matrix}\right.\)
P(2;3) là trung điểm của BC
=>\(\left\{{}\begin{matrix}x_B+x_C=2\cdot2=4\\y_B+y_C=2\cdot3=6\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}x_A+x_B=8\\x_A+x_C=10\\x_B+x_C=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_B-x_C=8-10=-2\\x_B+x_C=4\\x_A+x_C=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x_B=-2+4=2\\x_B+x_C=4\\x_A+x_C=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_B=\dfrac{2}{2}=1\\x_C=4-1=3\\x_A=10-3=7\end{matrix}\right.\)
Ta có: \(\left\{{}\begin{matrix}y_A+y_B=0\\y_A+y_C=4\\y_B+y_C=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y_B-y_C=-4\\y_B+y_C=6\\y_A+y_B=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2y_B=2\\y_B+y_C=6\\y_A=-y_B\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y_B=1\\y_C=6-1=5\\y_A=-1\end{matrix}\right.\)
Vậy: A(7;-1);B(1;1); C(3;5)
b: A(7;-1); P(2;3)
\(AP=\sqrt{\left(2-7\right)^2+\left(3+1\right)^2}=\sqrt{\left(-5\right)^2+4^2}=\sqrt{41}\)
c: A(7;-1)
Tọa độ điểm đối xứng với A qua trục Ox là:
\(\left\{{}\begin{matrix}x=x_A=7\\y=-y_A=1\end{matrix}\right.\)
Tọa độ điểm đối xứng với A qua trục Oy là:
\(\left\{{}\begin{matrix}x=-x_A=-7\\y=y_A=-1\end{matrix}\right.\)
e: E thuộc Ox nên E(x;0)
N(5;2);P(2;3); E(x;0)
\(\overrightarrow{NP}=\left(-3;1\right);\overrightarrow{NE}=\left(x-5;-2\right)\)
Để N,P,E thẳng hàng thì \(\dfrac{x-5}{-3}=\dfrac{-2}{1}\)
=>x-5=6
=>x=11
Vậy: E(11;0)

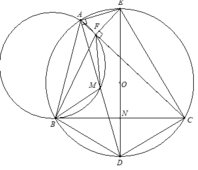
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).
\(\Delta CIM=\Delta AIN\left(c.g.c\right)\Rightarrow AN=MC\).
\(\Delta CIN=\Delta AIM\left(c.g.c\right)\)\(\Rightarrow NC=MA\).
Tam giác ABC vuông tại A có AM là đường trung tuyến nên CM = AM = MB.
Vì vậy NC = NA = AM = MC hay tứ giác NCMA là hình thoi, suy ra CA vuông góc với MN
Có IN = IM và MN vuông góc với CA nên M đối xứng với N qua AC.