Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương pháp: Độ lớn vận tốc cực đại vmax = ωA
Cách giải:
+ Ba lò xo giống hệt nhau, đều có độ cứng là k, khối lượng của các vật tương ứng là m1, m2 và m3
+ Kéo 3 lò xo ra khỏi VTCB một đoạn A rồi thả nhẹ => Biên độ dao động của chúng giống nhau và bằng A
+ Ta có:

+ Theo đề bài ta có:
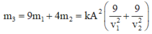
=> Vận tốc của con lắc 3 khi đi qua vị trí cân bằng:



Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Đáp án D
*Tốc độ cực đại khi đi qua VTCB là:
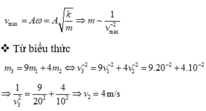
Bình luận: Phương pháp ở trên người ta gọi là phương pháp thuận nghịch.

Chọn trục toạ độ có gốc ở VTCB, chiều dương hướng sang phải.
Phương trình dao động tổng quát là: \(x=A\cos(\omega t+\varphi)\)
Theo thứ tự, ta lần lượt tìm \(\omega;A;\varphi\)
+ \(\omega=\sqrt{\dfrac{k}{m}}=20\sqrt 2(rad/s)\)
+ Biên độ A: \(A^2=x^2+\dfrac{v^2}{\omega^2}=3^2+\dfrac{(80\sqrt 2)^2}{(20\sqrt 2)^2}\)
\(\Rightarrow A = 5cm\)
+ Ban đầu ta có \(x_0=3cm\); \(v_0=-80\sqrt 2\) (cm/s) (do ta đẩy quả cầu về VTCB ngược chiều dương trục toạ độ)
\(\cos\varphi=\dfrac{x_0}{A}=\dfrac{3}{5}\); có \(v_0<0 \) nên \(\varphi > 0\)
\(\Rightarrow \varphi \approx0,3\pi(rad)\)
Vậy PT dao động: \(x=5\cos(20\sqrt 2+0,3\pi)(cm)\)

Ta có :
\(64^2_1x=36x^2_2=48^2\)
=> \(64x_1\le48^2\)
=> \(36x_2\le48^2\)
=> A1 = 6 (cm)
=> A2 = 8 (cm)
=> \(\frac{V_2}{V_1}=\frac{\omega\sqrt{A^2_2-x^2_2}}{\omega\sqrt{A^2_1-x^2_1}}=\frac{\sqrt{A^2_2-x^2_2}}{\sqrt{A^2_1-x^2_1}}=\frac{4}{3\sqrt{3}}\)
Vậy V2 = \(\frac{4.18}{3\sqrt{3}}=8\sqrt{3}\) (cm/giây)

Áp dụng:
+ \(A^2 = x^2 + \frac{v^2}{\omega^2} = 3^2+\frac{40^2}{\omega^2}\) (1)
+ Qua VTCB, vận tốc cực đại: \(v_{max} = \omega A \Rightarrow 50 = \omega A\) (2)
Từ (1) và (2) \(\Rightarrow \omega = 10 \ (rad/s); A = 5 \ cm\)
+ Khi vận tốc đạt giá trị v3 = 30cm/s, ta có: \(x = \pm\sqrt{A^2-\frac{v^2}{\omega^2}} = \pm 4 \ cm\)

Tốc độ của hệ hai vật khi đi qua vị trí cân bằng
\(V=V_{max}=\sqrt{\dfrac{k}{m_1+m_2}}.A_1=\sqrt{\dfrac{40}{2+2}}.10=10\pi\) cm/s
Khi đi qua vị trí cân bằng vật m1 (tấp độ của m1 cực đại khi đi qua vị trí cân bằng và giảm dần khi đến biên) và chuyển động thẳng đều với vận tốc v=vmax=\(10\pi\) cm/s
Biên độ dao động mới của vật m1 là \(A_2=\dfrac{V_{max}}{\sqrt{\dfrac{40}{2}}}=\dfrac{10\pi}{\sqrt{\dfrac{40}{2}}}\approx7cm\)
Lò xo dãn cực đại lần đầu tiên khi m1 đến biên tương ứng với khoảng thời gian \(\Delta t=\dfrac{T}{7}=\dfrac{2\pi}{7}.\sqrt{\dfrac{m_1}{k}}=\dfrac{2\pi}{7}.\sqrt{\dfrac{2}{40}}\approx\dfrac{1}{5}\left(s\right)\) kể từ thời điểm hai vật tách khỏi nhau
\(\Rightarrow\) Khoảng cách giữa hai vật \(\Delta x=v_{max}.\Delta t-A_2=...\)
Chúc bạn học tốt
Khi qua VTCB, tốc độ của con lắc đạt cực đại là:
\(v_{max}=\omega A =\sqrt{\dfrac{k}{m}}.A\)
\(\Rightarrow m = \dfrac{kA^2}{v_{max}^2}=\dfrac{a}{v_{max}^2}\) (vì \(kA^2=const\))
Theo đề bài ta có: \(m_3=9m_1+4m_2\)
\(\Rightarrow \dfrac{a}{v_3^2}=\dfrac{9a}{v_1^2}+\dfrac{4a}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{v_1^2}+\dfrac{4}{v_2^2}\)
\(\Rightarrow \dfrac{1}{v_3^2}=\dfrac{9}{20^2}+\dfrac{4}{10^2}\)
\(\Rightarrow v_3=4m/s\)
Chọn đáp án B.