Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
Tần số góc của dao động ω = k m = 100 0 , 1 = 10 π rad/s → T = 0,2 s
+ Ban đầu vật ở vị trí cân bằng, sau khoảng thời gian Δt = 0,75T = 0,15 s vật đến vị trí biên (lò xo bị nén cực đại) → Năng lượng của con lắc lúc này chỉ là thế năng đàn hồi của lò xo.
+ Giữ cố định điểm chính giữa của lò xo → một nửa thế năng bị mất đi → Năng lượng dao động lúc sau sẽ là:
E′ = 0,5E → 1 2 k ' A ' 2 = 0 , 5 1 2 k A 2
với k′ = 2k → A'= 0,5A.
ü Đáp án A

Động năng và thế năng của vật lại bằng nhau sau các khoảng thời gian
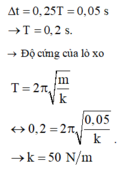
Đáp án A

Chọn A
+ Cứ sau khoảng thời gian T/4 thì động năng lại bằng thế năng
=> T/4 = 0,05 => T = 0,2s => ω = 10π rad/s.
+ Mà w= k m , thay m = 50g = 0,05kg và ω = 10π rad/s vào => k = 50 N/m.

Đáp án A
Động năng của vật bằng thế năng sau các khoảng thời gian t = 0,25T, vậy T = 0,2
→ Độ cứng của lò xo k = m ω 2 = m 2 π T 2 = 50 N/m

Giải thích: Đáp án A
Phương pháp: Sử dụng công thức tính vận tốc cực đại của vật dao động điều hoà
Cách giải:
| Ngay trước khi đặt thêm vật m2 |
Ngay sau khi đặt thêm vật m2 |
| VTCB: O Li độ: x = -A = -10 cm Vận tốc: v = 0 Tần số góc |
VTCB: O Li độ: x’ = -A = -10 cm Vận tốc: v’ = v = 0 Tần số góc
|
=> Sau đó hệ sẽ dao động với biên độ A’ = A = 10cm
+ Vận tốc cực đại của con lắc sau đó là 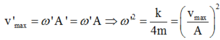
Do đó khối lượng m là: 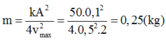
=> Chọn A

Đáp án D.
Gọi x là khoảng cách từ điểm giữ cố định tới điểm treo cố định, l là chiều dài khi bắt đầu giữ của lò xo. Nên khi này, ta được lò xo mới thực hiện dao động của vật với chiều dài 1-x lấy n = A x
Tại thời điểm giữ lò xo thì thế năng của nó là W t = W n 2
Khi giữ lò xo, phần thế năng bị mất đi là

Ta thấy, khi giữ thì 1 lò xo mới dao động với biên độ k' thỏa mãn
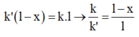
Bảo toàn cơ năng, ta có
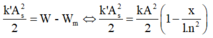
Do đó, ta có
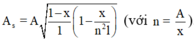
Giải ra được 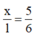
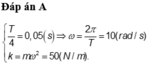

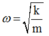
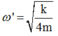

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)