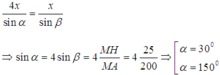Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B
![]()
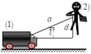
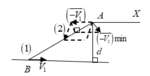
+ Đến (2) gặp được (1) điều kiện là v 21 → phải có hướng A B → .
+ Quỹ tích điểm ngọn A/ của v 1 , 2 → = A A ' → là 1 2 đường thẳng AB
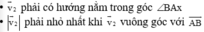
+ Tính chất đồng dạng của tam giác cho:
![]()

Đáp án B
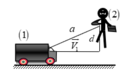
Xét chuyển động tương đối của (2) đối với (1) ta có:


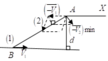
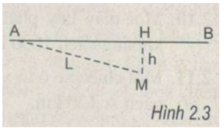
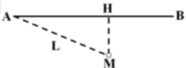
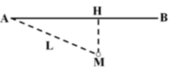
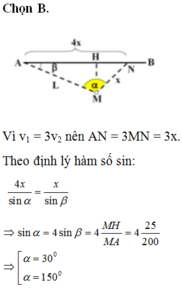
Giả sử người đó gặp ô tô tại điểm N. Khoảng thời gian t để người đó chạy từ M tới N phải đúng bằng khoảng thời gian để ô tô chạy từ A tới N
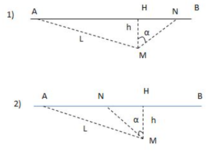
Ta có: AN = v 1 t = 36t
MN – v 2 t = 12t
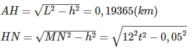
Cả hai trường hợp, đều có H N 2 = M N 2 - h 2
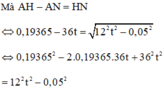
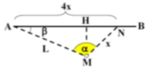
Cuối cùng ta được phương trình bậc hai 1152 t 2 – 13,9428t + 0,04 = 0
Giải ra ta được hai nghiệm: t = 0,00743h ≈ 26,7 s hoặc t = 0,00467h ≈ 16,8 s
Do đó AN = 0,26748 km hoặc AN = 0,16812 km
Quãng đường MN mà người ấy phải chạy là MN = 89,2 m hoặc MN = 56 m
Gọi α là góc hợp bởi MN và MH:

Vậy người đấy có thể chạy theo hai hướng để bắt xe với các góc là 55 ° 54 ' hoặc 26 ° 46 '

Chọn D.
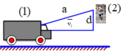
*Gọi vận tốc của A so với đường là vAC, vận tốc của B so với đường là vBC, vận tốc của B so với A là vBA.
Từ : vBC = vBA + vAC => 70 = vBA + 40 => vBA = 30 (km/h)

Đáp án B
Chọn hệ quy chiếu gắn với ô tô B, chiều dương là chiều chuyển động của hai ô tô :
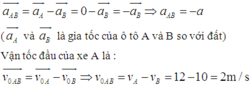
Dể không xảy ra va chạm giữa hai xe thì quãng đường xe A đi được từ lúc xe B bắt đầu tăng tốc đến lúc xe A dừng lại so với xe B là :
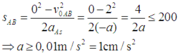

Bài 1.
Tóm tắt: \(a=2\)m/s2
\(S=16m\)
\(t=?\)
Bài giải:
\(S=\dfrac{1}{2}at^2\Rightarrow t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2\cdot16}{2}}=4s\)
Chọn A
Bài 2.
Tóm tắt: \(v_0=18\)km/h=5m/s
\(a=0,5\)m/s2
\(S=24m\)
\(v=?\)
Bài giải:
\(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot0,5\cdot24+5^2}=7\)m/s
Chọn C