Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Lần sau nếu đăng 2 bài bạn tách ra nhé cho dễ nhìn.
Bài 2.
Tóm tắt: \(v_0=18\)km/h=5m/s
\(a=0,5\)m/s2
\(S=24m\)
\(v=?\)
Bài giải:
Vận tốc xe sau: \(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot0,5\cdot24+5^2}=7\)m/s
Bài 1.
Gia tốc vật:
\(a=\dfrac{v^2-v^2_0}{2S}=\dfrac{2^2-0}{2\cdot16}=0,125\)m/s2
Bài 1:
Đổi 12km/h = 3,33m/s.
+) áp dụng công thức :
Vt^2-Vo^2 = 2a*s (1)
thay số ta được
0^2-3,33^2 = 2*10*a
=> a = -0,55(m/s^2)
=> Chọn D
Dạng 3:
Bài 2:
_Đổi đơn vị:
40 km/h =100/9 (m/s)
60 km/h =50/3 (m/s)
1 phút =60 (s)
* Ý 1:
- Áp dụng công thức: v = v₀+at
_Vì tàu bắt đầu rời ga=>v₀ = 0, v = 100/9 (m/s)
=>100/9 = 0+60a
<=>a≈ 0.185 (m/s²)=>chuyển động nhanh dần đều.
+Áp dụng công thức: v² - v₀² = 2aS
<=>(100/9)² =2(0.185)*S
<=>S= 1000/3 (m)
=> Chọn B
* Ý 2 :
- Nếu tiếp tục tăng tốc thì sau bao lâu tàu đạt vận tốc 60 km/h = 50/3 (m/s)
+Áp dụng công thức: v = v₀+at nhưng với v₀=100/9 (m/s) và v=50/3 (m/s)
=>t = v - v₀ / a = 50/3-100/9 / 0.185 ≈ 30(s) = 0,5 min
=> Chọn B
Chọn chiều dương là chiều chuyển động của ô tô, gốc tọa độ tại vị trí xuất phát, gốc thời gian là lúc xe ô tô khởi hành.
Đối với xe ô tô:
Vậy hai xe gặp nhau sau 40s và cách gốc là 400m
Vận tốc ô tô:
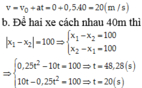
Đổi 36km/h = 10m/s
Gia tốc của xe:
Ta có: \(v=v_0+at\Leftrightarrow a=\dfrac{v-v_0}{t}=\dfrac{15-10}{5}=1\left(m/s^2\right)\)
Vận tốc của xe ở giây thứ 10:
\(v=v_0+at=10+1.10=20\left(m/s\right)\)
m/s trên đoạn đường thẳng thì người lái xe tăng ga và xe chuyển động nhanh dần đều. Sau 
ô tô đạt vận tốc 
m/s. Quảng đường mà ô tô đi được sau 
s kể từ lúc bắt đầu tăng ga là
Gia tốc vật: \(v=v_0+at\)
\(\Rightarrow a=\dfrac{v-v_0}{t}=\dfrac{15-5}{20}=0,5\)m/s2
Quãng đường xe sau 20s tăng ga:
\(S=v_0t+\dfrac{1}{2}at^2=5\cdot20+\dfrac{1}{2}\cdot0,5\cdot20^2=200m\)
Chọn đáp án D
− Gia tốc của ôtô: a = v − v 0 Δ t = 0 , 2 m / s 2
− Quãng đường xe đi được sau 40 s từ lúc tăng ga: s = v 0 t + 1 2 a t 2 = 560 m
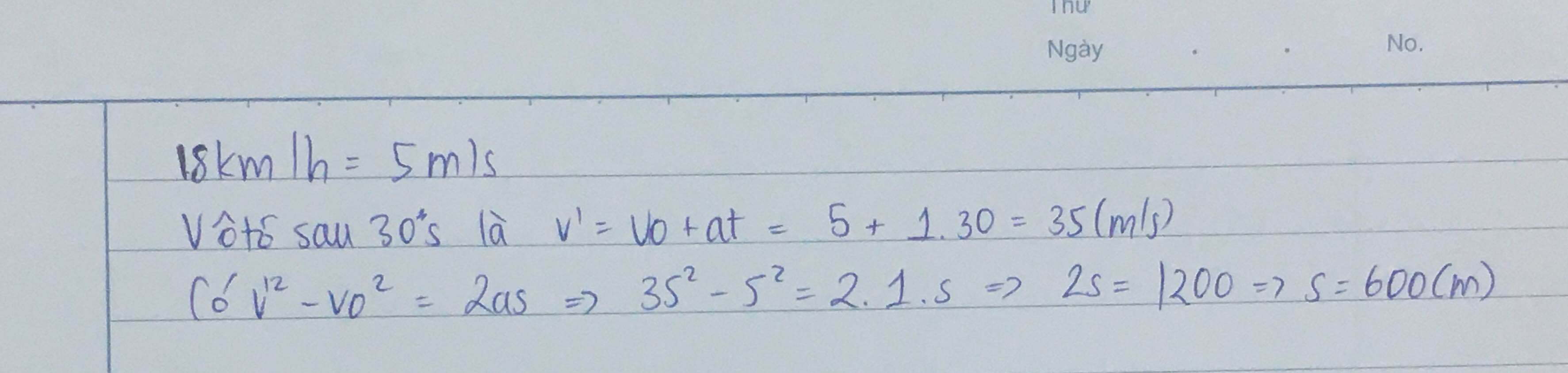
Bài 1.
Tóm tắt: \(a=2\)m/s2
\(S=16m\)
\(t=?\)
Bài giải:
\(S=\dfrac{1}{2}at^2\Rightarrow t=\sqrt{\dfrac{2S}{a}}=\sqrt{\dfrac{2\cdot16}{2}}=4s\)
Chọn A
Bài 2.
Tóm tắt: \(v_0=18\)km/h=5m/s
\(a=0,5\)m/s2
\(S=24m\)
\(v=?\)
Bài giải:
\(v^2-v^2_0=2aS\)
\(\Rightarrow v=\sqrt{2aS+v^2_0}=\sqrt{2\cdot0,5\cdot24+5^2}=7\)m/s
Chọn C