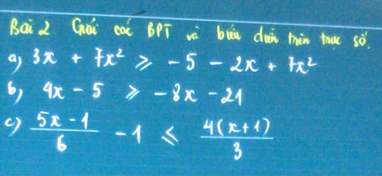Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 2:
a: Xét ΔBAC có BE/BA=BF/BC
nên EF//AC và EF=AC/2
Xét ΔDAC có DG/DC=DH/DA
nên HG//AC và HG=AC/2
=>EF//HG và EF=HG
=>EFGH là hình bình hành
b: Xét ΔDAB có DH/DA=DN/DB
nên HN//AB và HN=AB/2
Xét ΔCAB có CM/CA=CF/CB
nên MF//AB và MF=AB/2
=>HN//MF và HN=MF
=>HNFM là hình bình hành
=>HF cắt NM tại trung điểm của mỗi đường
=>O là trung điểm của MN

Bài 1:
a.Xét tam giác PNM và tam giác PQR ,ta có :
A^=Q^(= 90 độ )
P1^= P2^(đối đỉnh )
=>tam giác PNMđồng dạng tam giác PQR
b.ta có: MN//PR
=>NPtrên PQ=MN trên QR
=>x=3 nhân 6 trên 2
=>x=9

a, \(3x+7x^2+5+2x-7x^2\ge0\Leftrightarrow5x+5\ge0\Leftrightarrow x\ge-1\)
b, \(12x\ge-16\Leftrightarrow x\ge-\dfrac{4}{3}\)
c, \(\dfrac{5x-1-6}{6}-\dfrac{4\left(x+1\right)}{3}\le0\)
\(\Leftrightarrow\dfrac{5x-7-8\left(x+1\right)}{6}\le0\Rightarrow-3x-15\le0\Leftrightarrow x\le-5\)

a: ΔABC cân tại A
mà AH là đường cao
nên H là trung điểm của BC
Xét tứ giác ABDC có
H là trung điểm chung của AD và BC
nên ABDC là hình bình hành
Hình bình hành ABDC có AB=AC
nên ABDC là hình thoi
b: H là trung điểm của BC
=>\(HB=HC=\dfrac{BC}{2}=3\left(cm\right)\)
ΔAHB vuông tại H
=>\(AH^2+HB^2=AB^2\)
=>\(AH^2=5^2-3^2=16\)
=>AH=4(cm)
AD=2*AH
=>AD=2*4=8(cm)
c:
Xét tứ giác AHCF có
E là trung điểm chung của AC và HF
nên AHCF là hình bình hành
Hình bình hành AHCF có \(\widehat{AHC}=90^0\)
nên AHCF là hình chữ nhật
=>AH\(\perp\)AF và HC\(\perp\)FC
d: ABDC là hình thoi
=>\(\widehat{BAC}=\widehat{BDC}=60^0\)
ABDC là hình thoi
=>\(\widehat{ABD}+\widehat{BAC}=180^0\)
=>\(\widehat{ABD}=120^0\)
ABDC là hình thoi
=>\(\widehat{ABD}=\widehat{ACD}=120^0\)

a/(b+c) + b/(a+c) + c/(a+b) = a^2/(ab+ac) + b^2/(ba+bc) + c^2/(ac+bc) >=
(a+b+c)^2/(2.(ab+bc+ac) (buhihacopxki dạng phân thức)
>= (3.(ab+bc+ac)/(2(ab+bc+ac) =3/2
a^2/(b^2+c^2) + b^2/(a^2+c^2) + c^2/(a^2+b^2) >= (a+b+c)^2/(2.(a^2+b^2+c^2) (buhihacopxki dạng phân thức)
>= 3(a^2+b^2+c^2) / 2(a^2+b^2+c^2) >=3/2
\(\Leftrightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}-\dfrac{3}{2}\ge0\)
\(\Leftrightarrow\left(\dfrac{a}{b+c}-\dfrac{1}{2}\right)+\left(\dfrac{b}{c+a}-\dfrac{1}{2}\right)+\left(\dfrac{c}{a+b}-\dfrac{1}{2}\right)\ge0\)
\(\Leftrightarrow\left(\dfrac{2a-b-c}{2\left(b+c\right)}\right)+\left(\dfrac{2b-a-c}{2\left(a+c\right)}\right)+\left(\dfrac{2c-a-b}{2\left(a+b\right)}\right)\ge0\)
\(\Leftrightarrow\dfrac{a-b+a-c}{2\left(b+c\right)}+\dfrac{b-a+b-c}{2\left(a+c\right)}+\dfrac{c-a+c-b}{2\left(a+b\right)}\ge0\)
\(\Leftrightarrow\dfrac{a-b}{2\left(b+c\right)}+\dfrac{a-c}{2\left(b+c\right)}+\dfrac{b-a}{2\left(a+c\right)}+\dfrac{b-c}{2\left(a+c\right)}+\dfrac{c-a}{2\left(a+b\right)}+\dfrac{c-b}{2\left(a+b\right)}\ge0\)\(\Leftrightarrow\left(a-b\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+c\right)}\right]+\left(a-c\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]+\left(b-c\right)\left[\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\)
ta có: a,b,c là 3 số dương bất kì nên ta giả sử \(a\ge b\ge c\)
\(\Rightarrow a+c\ge b+c\)
\(\Leftrightarrow2\left(a+c\right)\ge2\left(b+c\right)\)
\(\Leftrightarrow\dfrac{1}{2\left(a+c\right)}\le\dfrac{1}{2\left(b+c\right)}\)
\(\Leftrightarrow\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(b+c\right)}\ge0\)
Mà \(a\ge b\Rightarrow a-b\ge0\)
\(\Rightarrow\left(a-b\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+c\right)}\right]\ge0\left(1\right)\)
Chứng minh tương tự, ta có:
\(\left(a-c\right)\left[\dfrac{1}{2\left(b+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\left(2\right)\)
\(\left(b-c\right)\left[\dfrac{1}{2\left(a+c\right)}-\dfrac{1}{2\left(a+b\right)}\right]\ge0\left(3\right)\)
Cộng từng vế (1);(2);(3) \(\Rightarrow\) luôn đúng
\(\Rightarrow\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\ge\dfrac{3}{2}\)


Tôi làm tạm theo cách này nhé.
\(x^4-2x^2-114x-1295\)
\(=\frac{d}{dx}\left(x^4-2x^2-114x-1295\right)\)
\(=4x^3-4x-114-0\)
\(=4x^3-4x-114\)
Bạn Phương Lê Nhật ơi!!!!
Đây là Toán 8 bạn ạ
Bạn giải mk ko hiểu j cả
Giải cụ thể đc ko bạn ạ
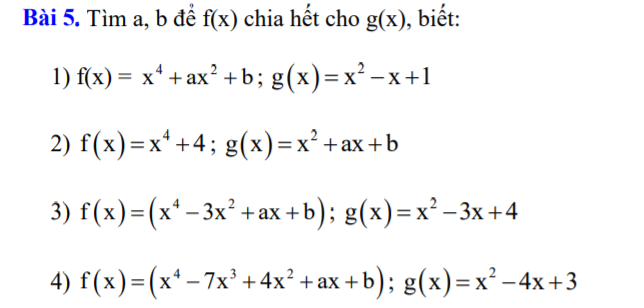
 nhờ các cao nhân giúp mik bài 2 ạ =))
nhờ các cao nhân giúp mik bài 2 ạ =))