nhờ các bạn giúp mnhf với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
13 tháng 12 2021
Lời giải:
Gọi số công nhân mỗi đội lần lượt là $a,b,c$. Vì số công nhân tỉ lệ nghịch với số
ngày làm nên $4a=6b=8c=\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}$
Áp dụng TCDTSBN:
$\frac{a}{\frac{1}{4}}=\frac{b}{\frac{1}{6}}=\frac{c}{\frac{1}{8}}=\frac{a-b}{\frac{1}{4}-\frac{1}{6}}=\frac{4}{\frac{1}{12}}=48$
$\Rightarrow a=48.\frac{1}{4}=12; b=48.\frac{1}{6}=8; c=48.\frac{1}{8}=6$
SH
4
NK
1
2 tháng 1 2017
|x-1|=12-|2x-6|
x-1=(12...6|)hoặc-(12....2x-6|)
TH1:x-1=12-|2x-6| TH2 như thế chỉ khác là âm thôi
|2x-6|=12-x+1 (chuyển vế đổi dấu)
2x-6=12-x+1 hoặc-(12-x+1)
Nếu 2x-6=12-x+1 Nếu 2x-6=- (12-x+1)
Tự làm nha tự làm nha
24 tháng 6 2016
(x^2+1)(x-1)(x+3)>0
Vì x^2+1>0 với mọi x
nên: (x-1)(x+3)>0
Trường hợp 1:
x-1<0, x+3 <0
Vì x+3 > x-1 nên x+3<0 suy ra x<-3
Trường hợp 2:
x-1>0, x+3>0
Vì x-1<x+3 nên x-1 >0 suy ra x>1
Vậy x<-3 hoặc x>1
24 tháng 6 2016
Vì tích 3 số là số dương nên trong 3 số có thể gồm 2 số âm, 1 số dương hoặc cả 3 số đều dương
TH1: Có 2 số âm, 1 số dương
Trước hết ta có \(x+3>x-1\)
\(x^2+1>x-1\)
Vì vậy \(x-1< 0\)
\(x^2+1>0\) nên \(x+3< 0\)
\(\Rightarrow x< -3\left(< 1\right)\)
TH2: Cả 3 số đều dương
Xét số bé nhất lớn hơn 0:
\(x-1>0\Rightarrow x>1\)
Vậy \(\orbr{\begin{cases}x< -3\\x>1\end{cases}}\)
JW
1
15 tháng 6 2023
a: góc ABM=góc AEF
góc AMB=góc AFE
mà góc AEF=góc AFE
nên góc ABM=góc AMB
=>ΔABM cân tại A
b: Kẻ BN//FC
Xét ΔBDN và ΔCDF có
góc DBN=góc DCF
DB=DC
góc BDN=góc CDF
=>BN=FC
góc BNE=góc AFE
=>góc BNE=góc BEN
=>BN=BE=FC=MF
LM
0
26 tháng 6 2019
\(\frac{x}{2}-\frac{3x}{5}=\frac{-7}{5}+\frac{7x}{10}\)
\(\Leftrightarrow\frac{5x}{10}-\frac{6x}{10}-\frac{7x}{10}=\frac{-7}{5}\)
\(\Leftrightarrow\frac{-8x}{10}=\frac{-7}{5}\)
\(\Leftrightarrow-8x=-14\)
\(\Leftrightarrow x=\frac{7}{4}\)
Vậy...
13 tháng 7 2020
Công thức này bạn ko cần chứng minh lại nhé !
\(1+2+3+.....+n=\frac{n\left(n+1\right)}{2}\)
Áp dụng với n = 99 ta có:
\(1+2+3+....+98+99=\frac{98\cdot\left(99+1\right)}{2}=4900\)
Vậy B=4900
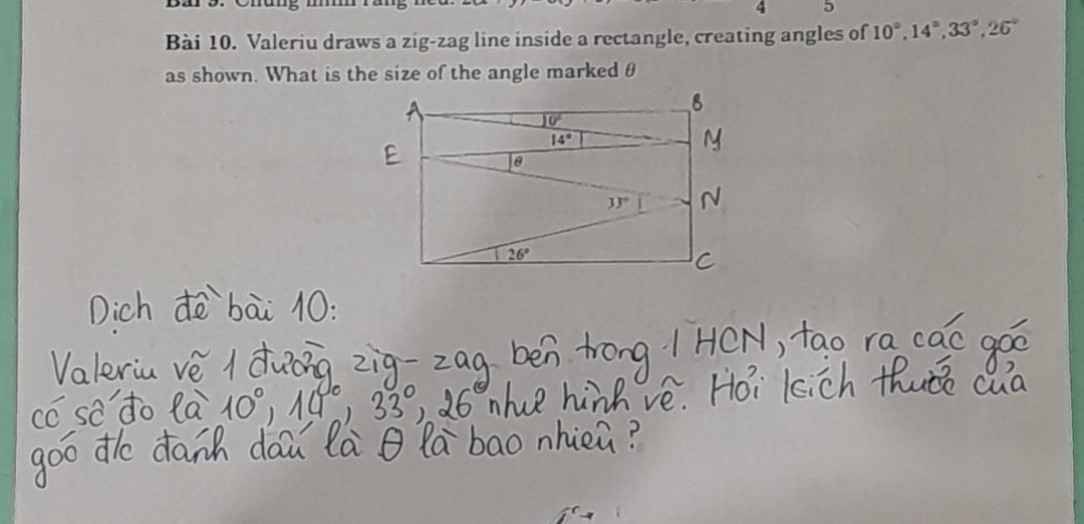
Bài 1. Đặt \(A=\left(a^2-1\right)\left(a^2-4\right)\left(a^2-7\right)\left(a^2-10\right)\)
Xét với \(a\)nguyên:
Với \(a=0\): \(\left(0-1\right)\left(0-4\right)\left(0-7\right)\left(0-10\right)=1.4.7.10>0\)không thỏa mãn.
Với \(a^2=1\): \(A=0\)không thỏa.
Vơi \(a^2=4\): \(A=0\)không thỏa.
Với \(a^2=9\): \(A=\left(9-1\right)\left(9-4\right)\left(9-7\right)\left(9-10\right)< 0\)thỏa mãn.
Với \(a^2>9\)suy ra \(a^2\ge16\)khi đó dễ thấy \(A>0\)không thỏa.
Vậy \(a^2=9\Leftrightarrow a=\pm3\).
Bài 2:
b) \(D=\left(x+2y-3\right)^2+5\left|y+3\right|-2\ge-2\)
Dấu \(=\)khi \(\hept{\begin{cases}x+2y-3=0\\y+3=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=9\\y=-3\end{cases}}\).
d) \(F=\frac{1}{\left(x-2y+3\right)^2+1}-\left|y^2-1\right|+3\le3\)
Dấu \(=\)khi \(\hept{\begin{cases}x-2y+3=0\\y^2-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1,y=1\\x=-5,y=-1\end{cases}}\).