
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(-\dfrac{9}{19}>-\dfrac{10}{19}>-\dfrac{10}{21}\\ \Rightarrow-\dfrac{9}{19}>-\dfrac{10}{21}\)

Ta có \(A=\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\)
\(2A=1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\)
\(2A-A=\left(1+\dfrac{2}{2}+\dfrac{3}{2^2}+...+\dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac{1}{2}+\dfrac{2}{2^2}+\dfrac{3}{2^3}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\right)\)\(A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\) - \(\dfrac{2023}{2^{2023}}\)
Đặt B = \(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\)
2B = \(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\)
2B - B = \(\left(2+1+\dfrac{1}{2}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)-\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\right)\)B = 2 - \(\dfrac{1}{2^{2022}}\)
Suy ra A = 2 - \(\dfrac{1}{2^{2022}}\) - \(\dfrac{2023}{2^{2023}}\) < 2
Vậy A < 2
\(A=\dfrac{1}{2}+\dfrac{2}{2^{2}}+\dfrac{3}{2^{3}}+...+\dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\)
\(2A=1+\dfrac22+\dfrac3{2^2}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\\2A-A=\left(1+\dfrac22+\dfrac3{2^2}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2021}}+\dfrac{2023}{2^{2022}}\right)-\left(\dfrac12+\dfrac2{2^2}+\dfrac3{2^3}\ +\,.\!.\!.+\ \dfrac{2022}{2^{2022}}+\dfrac{2023}{2^{2023}}\right)\\A=1+\dfrac12+\dfrac1{2^3}\ +\,.\!.\!.+\ \dfrac1{2^{2021}}+\dfrac1{2^{2022}}-\dfrac{2023}{2^{2023}}\\2\left(A+\dfrac{2023}{2^{2023}}\right)=2+1+\dfrac12+\dfrac1{2^2}\ +\,.\!.\!.+\ \dfrac1{2^{2020}}+\dfrac1{2^{2021}}\\A+\dfrac{2023}{2^{2023}}=2-\dfrac1{2^{2022}}\\A=2-\dfrac1{2^{2022}}+\dfrac{2023}{2^{2023}}<2\)

Công thức này bạn ko cần chứng minh lại nhé !
\(1+2+3+.....+n=\frac{n\left(n+1\right)}{2}\)
Áp dụng với n = 99 ta có:
\(1+2+3+....+98+99=\frac{98\cdot\left(99+1\right)}{2}=4900\)
Vậy B=4900

1: Xét ΔABM và ΔDBM có
BA=BD
BM chung
MA=MD
Do đó: ΔABM=ΔDBM
2: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó:ΔBAE=ΔBDE
Suy ra: \(\widehat{BAE}=\widehat{BDE}=90^0\)
hay DE⊥BC
3: Xét ΔAME và ΔDME có
EA=ED
\(\widehat{AEM}=\widehat{DEM}\)
EM chung
Do đó: ΔAME=ΔDME

\(\left|3x-4\right|-\left|y+3\right|=0\)
\(\Rightarrow\left|3x-4\right|+\left|3-y\right|=0\)
\(\Rightarrow\hept{\begin{cases}3x-4=0\\3-y=0\end{cases}\Rightarrow\hept{\begin{cases}x=\frac{4}{3}\\y=3\end{cases}}}\)

\(1,\\ a,A_1=\left(x-2\right)^2+5\ge5\)
Dấu \("="\Leftrightarrow x=2\)
\(A_2=\left(x+1\right)^2+7\ge7\)
Dấu \("="\Leftrightarrow x=-1\)
\(A_3=\left(3-2x\right)^2-1\ge-1\)
Dấu \("="\Leftrightarrow x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(b,B_1=\left|x-2\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_2=\left|x+1\right|+3\ge3\)
Dấu \("="\Leftrightarrow x=-1\)
\(B_3=\left|2x-4\right|-3\ge-3\)
Dấu \("="\Leftrightarrow x=2\)
\(B_4=\left|6x+1\right|-20\ge-20\)
Dấu \("="\Leftrightarrow x=-\dfrac{1}{6}\)
Bài 1:
a: \(A_1=\left(x-2\right)^2+5\ge5\forall x\)
Dấu '=' xảy ra khi x=2
\(A_2=\left(x+1\right)^2+7\ge7\forall x\)
Dấu '=' xảy ra khi x=-1
\(A_3=\left(3-2x\right)^2-1\ge-1\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{2}\)
\(A_4=\left(x-2\right)^2-3\ge-3\forall x\)
Dấu '=' xảy ra khi x=2
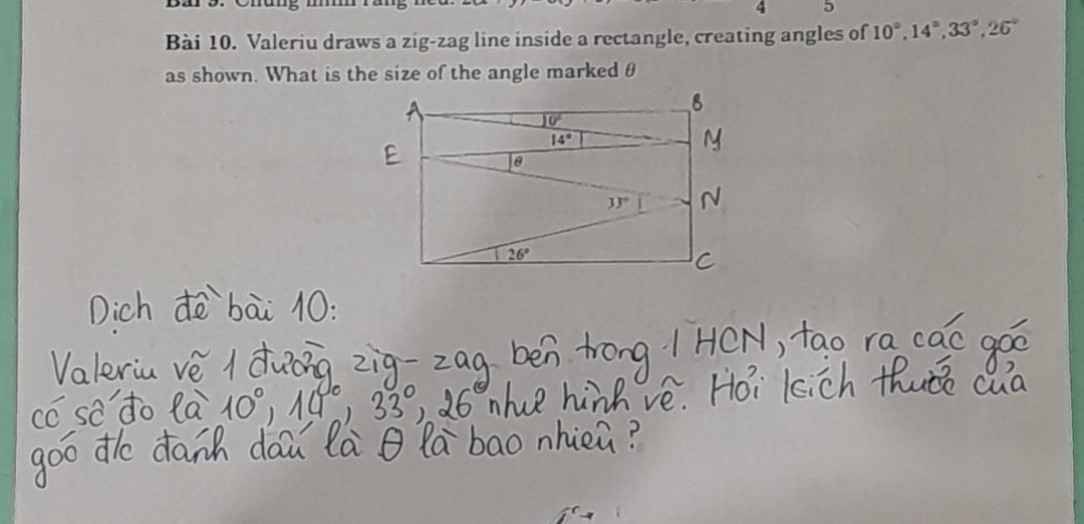
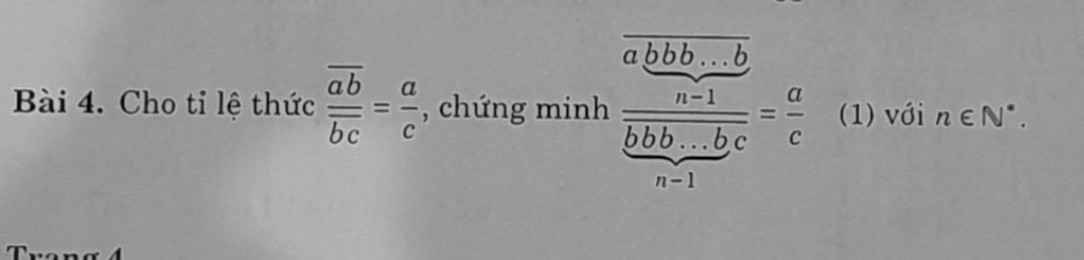

 Các bạn giúp mk mỗi bài 1 hoi ạ:))
Các bạn giúp mk mỗi bài 1 hoi ạ:))