Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\( b)2000 - M = 2000 - \dfrac{1}{{1 - \sqrt x + x}}\\ x - \sqrt x + 1 = x - 2\sqrt x .\dfrac{1}{2} + \dfrac{1}{4} + \dfrac{3}{4} = {\left( {\sqrt x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \)
Với \(x \ge 4\) \(\Rightarrow \sqrt x \ge 2\)
\( \Rightarrow \sqrt x - \dfrac{1}{2} \ge \dfrac{3}{2}\\ \Rightarrow {\left( {\sqrt x - \dfrac{1}{2}} \right)^2} \ge \dfrac{9}{4}\\ \Rightarrow {\left( {\sqrt x - \dfrac{1}{2}} \right)^2} + \dfrac{3}{4} \ge \dfrac{9}{4} + \dfrac{3}{4} = 3\\ \Rightarrow x - \sqrt x + 1 \ge 3\\ \Rightarrow \dfrac{1}{{1 - \sqrt x + x}} \le \dfrac{1}{3}\\ \Rightarrow 2000 - \dfrac{1}{{1 - \sqrt x + x}} \ge 2000 - \dfrac{1}{3} = \dfrac{{5999}}{3} \)
Vậy với \(x \ge 4\) thì $Min$ \(2000 - M = \dfrac{{5999}}{3}\) khi và chỉ khi \(x=4\)
$c)$ \(M = \dfrac{1}{{1 - \sqrt x + x}}\)
Để $M$ nguyên \(\Rightarrow1-\sqrt{x}+x\inƯ\left(1\right)=\left\{1;-1\right\}\)
\(\Rightarrow\left\{{}\begin{matrix}1-\sqrt{x}+1=1\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\\1-\sqrt{x}+1=-1\Leftrightarrow x-\sqrt{x}+2=0\left(VN\right)\end{matrix}\right.\)
Vậy \(x=1\) hoặc \(x=0\) thì $M$ nguyên

bạn ghi rõ nội dung, yêu cầu đề của bài đó ra cho mình nha

\(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{x-3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(\Rightarrow B=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)
\(\dfrac{2x+3\sqrt{x}+9-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\left(\sqrt{x}+3\right)^2}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)

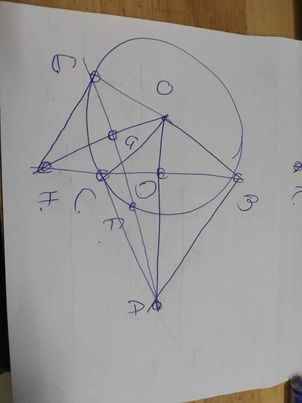
Cho đường tròn (O;R) đường kính AB trên tiếp tuyến của đường tròn O tại lấy điểm M từ M vẽ tiếp tuyến thứ hai MC với đường tròn O ,C là tiếp điểm .Kẻ CH vuông góc với AB ,MB cắt đường tròn O tại điểm thứ hai là K và cắt CH tại N .Chứng minh rằng
a) Chứng minh AM bình=MK.MB
b)Cho biết R=5cm,góc AMC=60 độ .tính độ dài AM
c)Chứng minh góc KAC=góc OMB
d)Chứng minh N là trung điểm của CH
Mình viết mải quá nên thiếu các bạn vào làm hộ mik với nhé

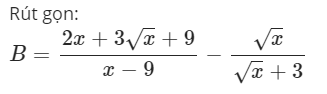
Xin lỗi bạn.
Mình mới học lớp 8 thôi