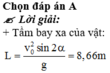Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1.
Sau khi bắn 0,1s ta có:
Vận tốc ném theo phương ngang: \(v_1=v_0cos\alpha=4\cdot cos45=2\sqrt{2}m/s\)
Vận tốc ném theo phương thẳng đứng:
\(v_2=v_0sin\alpha-gt=4\cdot sin45-10\cdot0,1=2\sqrt{2}-1\approx1,83m/s\)
Sau khi bắn 0,2s ta có:
Theo phương ngang: \(v_1'=v_0cos\alpha=4\cdot cos45=2\sqrt{2}m/s\)
Theo phương thẳng đứng:
\(v_2'=v_0sin\alpha-gt=4\cdot sin45-10\cdot0,2=2\sqrt{2}-2\approx0,83m/s\)
Câu 2.
a)Thời gian viên bi đạt tầm cao H:
\(t=\dfrac{v_0\cdot sin\alpha}{g}=\dfrac{4\cdot sin45}{10}=\dfrac{\sqrt{2}}{5}\approx0,28s\)
Tầm cao H: \(H=\dfrac{v_0^2\cdot sin^245}{2g}=\dfrac{4^2\cdot0,5}{2\cdot10}=0,4m\)
Vận tốc vật từ lúc nhảy đến khi đạt độ cao H là:
\(v=v_0-gt=4-10\cdot\dfrac{\sqrt{2}}{5}=4-2\sqrt{2}\left(m/s\right)\)
Gia tốc bi ở tầm H là: \(a=\dfrac{v^2-v_0^2}{2S}=\dfrac{\left(4-2\sqrt{2}\right)^2-4^2}{2\cdot0,4}=-18,3m/s^2\)
Câu 3.
a)Vận tốc của viên bi có độ lớn cực tiểu ở vị trí tầm cao:
b)Thời điểm tại lúc đó: \(t=2\cdot\dfrac{v_{0y}}{g}=2\cdot\dfrac{v_0\cdot sin45}{10}=\dfrac{2\sqrt{2}}{5}s\)
Câu 4.
a)Khi viên bi chạm sàn thì thời gian chuyển động là \(t=\dfrac{2\sqrt{2}}{5}s\)
\(v_{0x}=v_0cos\alpha=4\cdot cos45=2\sqrt{2}m/s\)
\(v_{0y}=v_0\cdot sin\alpha=4\cdot sin45=2\sqrt{2}m/s\)
Vận tốc viên bi khi chạm sàn: \(v=\sqrt{v_{0x}^2+v_{0y}^2}=4m/s\)
b)Giống câu a
c)Tầm xa L của bi: \(L=\dfrac{v_0^2\cdot sin^22\alpha}{g}=\dfrac{4^2\cdot\left(sin90\right)^2}{10}=1,6m\)

) Để tính tỉ số giữa độ cao cực đại và tầm xa của vật, ta cần tìm độ cao cực đại và tầm xa của vật. Độ cao cực đại (hmax) được tính bằng công thức: hmax = (v0^2 * sin^2(α)) / (2g) Tầm xa (R) được tính bằng công thức: R = (v0^2 * sin(2α)) / g Với α = 45°, ta có: hmax = (v0^2 * sin^2(45°)) / (2 * 10) = (v0^2 * 1/2) / 20 = v0^2 / 40 R = (v0^2 * sin(2 * 45°)) / 10 = (v0^2 * sin(90°)) / 10 = (v0^2 * 1) / 10 = v0^2 / 10 Tỉ số giữa độ cao cực đại và tầm xa của vật là: hmax / R = (v0^2 / 40) / (v0^2 / 10) = (10 * v0^2) / (40 * v0^2) = 1/4 Vậy tỉ số giữa độ cao cực đại và tầm xa của vật là 1/4. b) Để độ cao cực đại bằng với tầm xa của vật, ta cần giải phương trình: hmax = R (v0^2 / 40) = (v0^2 / 10) Với v0^2 khác 0, ta có: 1/40 = 1/10 Điều này là không thể xảy ra, vì vậy không tồn tại góc α để độ cao cực đại bằng với tầm xa của vật

1.
+ Vận tốc ban đầu của viên bi theo phương ngang: \({v_{0x}} = {v_0}.\cos \alpha = 4.\cos {45^0} = 2\sqrt 2 (m/s)\)
+ Vận tốc ban đầu của viên bi theo phương thẳng đứng: \({v_{0y}} = {v_0}.\sin \alpha = 4.\sin {45^0} = 2\sqrt 2 (m/s)\)
+ Vận tốc của viên bi theo phương ngang sau 0,1 s và sau 0, 2 s là \({v_{0x}} = 2\sqrt 2 m/s\)
+ Vận tốc của viên bi theo phương thẳng đứng sau 0,1 s là: \({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8.0,1 \approx 1,85(m/s)\)
+ Vận tốc của viên bi theo phương thẳng đứng sau 0,2 s là:
\({v_y} = {v_{0y}} - gt = 2\sqrt 2 - 9,8.0,2 \approx 0,87(m/s)\)
2.
a) Thời gian viên bi đạt tầm cao H: \(t = \frac{{{v_{0y}}}}{g} = \frac{{2\sqrt 2 }}{{9,8}} \approx 0,29(s)\)
b) Tầm cao H là: \(H = \frac{{v_{0y}^2}}{{2.g}} = \frac{{{{(2\sqrt 2 )}^2}}}{{2.9,8}} \approx 0,4(m)\)
c) Gia tốc của viên bi ở tầm cao H là: a = g = 9,8 (m/s2 )

a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :


Giải :
a. Chọn chiều dương là chiều hướng từ trên xuống dưới, gốc tọa độ tại vị trí viên bi A, gốc thời gian là lúc viên bi A rơi
Phương trình chuyển động :