Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


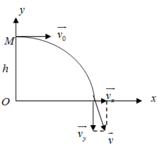
a. Chọn hệ quy chiếu Oxy như hình vẽ
Thời điểm ban đầu
Chiếu lên trục ox có
x 0 = 0 ; v 0 x = v 0 c o s α = 10 2 ( m / s )
Chiếu lên trục oy có
y 0 = 0 ; v 0 y = v 0 s i n α = 10 √ 2 ( m / s )
Xét tại thời điểm t có a x = 0 ; a y = - g
Chiếu lên trục ox có
v x = 10 √ 2 ( m / s ) ; x = 10 √ 2 t
Chiếu lên trục Oy có
v y = 10 √ 2 - 10 t ; y = 45 + 10 √ 2 t - 5 t 2
⇒ y = 45 + x - x 2 40 Vậy vật có quỹ đạo là một Parabol
Khi lên đến độ cao max thì: v y = 0 ⇒ 0 = 10 √ 2 - 10 t ⇒ t = √ 2 ( s )
H m a x = y = 45 + 10 . √ 2 . √ 2 - 5 ( √ 2 ) 2 = 55 ( m )
Khi vật chạm đất thì y = 0 ⇒ 45 + 10 √ 2 t - 5 t 2 = 0 ⇒ t = 4 , 73 ( s )
Vậy sau 4,73s thì vật chạm đất
b. Tầm xa của vật L = x = 10 √ 2 . 4 , 73 ≈ 66 , 89 ( m )
Vận tốc vật khi chạm đất v = v x 2 + v y 2
Với v y = 10 √ 2 - 10 . 4 , 73 = 33 , 16 ( m / s )
⇒ v = √ ( ( 10 √ 2 ) 2 + 33 , 〖 16 〗 2 ) = 36 , 05 ( m / s )
c. Khi vật có độ cao 50 thì
y = 50 = 45 + 10 √ 2 t - 5 t 2 ⇒ t 1 = 2 , 414 ( s ) ; t 2 = 0 , 414 ( s )
Lúc t 1 = 2 , 414 ( s ) ⇒ v 1 = 10 √ 2 - 10 t 1 = 10 √ 2 - 10 . 2 , 414 ≈ - 10 ( m / s )
Lúc t 2 = 0 , 414 ( s ) ⇒ v 2 = 10 √ 2 - 10 t 2 = 10 √ 2 - 10 . 0 , 414 ≈ 10 ( m / s )
Ứng với hai trường hợp vật đi xuống đi lên

Cơ năng vật ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot m\cdot3^2+m\cdot10\cdot0=\dfrac{9}{2}m\left(J\right)\)
Cơ năng vật tại nơi có độ cao \(h_{max}\) là \(W_1=mgh_{max}\left(J\right)\)
Bảo toàn cơ năng :\(W=W_1\)
\(\Rightarrow\dfrac{9}{2}m=mgh_{max}\Rightarrow h_{max}=0,45m\)
Cơ năng vật tại nơi có \(W_đ=W_t\):
\(W_2=W_đ+W_t=2W_đ=2\cdot\dfrac{1}{2}mv'^2=mv'^2\left(J\right)\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow\dfrac{9}{2}m=mv'^2\Rightarrow v'=\dfrac{3\sqrt{2}}{2}\)m/s

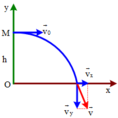
a.Chọn hệ quy chiếu Oxy với O là ở mặt đất
+ Trên trục Ox ta có :
a x = 0 ; v x = v 0 ; x = v 0 t
+ Trên trục Oy ta có :
a y = - g ; v y = - g t = - 10 t
y = h − 1 2 g t 2 = 125 − 5 t 2
Khi vật chạm đất
y = 0 ⇒ 125 − 5 t 2 = 0 ⇒ t = 5 s
Tầm xa của vật
L = x max = v 0 . t = 120 m ⇒ v 0 = 24 m / s
b. Vận tốc của vật khi chạm đất v = v x 2 + v y 2
Với v x = 24 m / s ; v y = − 10.5 = − 50 m / s
⇒ v = 24 2 + 50 2 = 55 , 462 m / s


v = v x 2 + v y 2 → v x = 24 m / s v y = − 10.5 = − 50 m / s v = 24 2 + 50 2 = 55 , 462 m / s

Vật chỉ chịu tác dụng của trọng lực cơ năng được bảo toàn:
Bảo toàn tại điểm ném W1 và tại điểm chạm đất W2 ( Chọn gốc thế năng tại mặt đất )
\(W_1=W_2\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz=\dfrac{1}{2}mv_2^2\) => z=25(m)
b) Bảo toàn cơ năng tại điểm ném và vị trí cao nhất:
\(W_1=W_3\Leftrightarrow\dfrac{1}{2}mv_1^2+mgz=mgh_{max}\Rightarrow h_{max}=45\left(m\right)\)



) Để tính tỉ số giữa độ cao cực đại và tầm xa của vật, ta cần tìm độ cao cực đại và tầm xa của vật. Độ cao cực đại (hmax) được tính bằng công thức: hmax = (v0^2 * sin^2(α)) / (2g) Tầm xa (R) được tính bằng công thức: R = (v0^2 * sin(2α)) / g Với α = 45°, ta có: hmax = (v0^2 * sin^2(45°)) / (2 * 10) = (v0^2 * 1/2) / 20 = v0^2 / 40 R = (v0^2 * sin(2 * 45°)) / 10 = (v0^2 * sin(90°)) / 10 = (v0^2 * 1) / 10 = v0^2 / 10 Tỉ số giữa độ cao cực đại và tầm xa của vật là: hmax / R = (v0^2 / 40) / (v0^2 / 10) = (10 * v0^2) / (40 * v0^2) = 1/4 Vậy tỉ số giữa độ cao cực đại và tầm xa của vật là 1/4. b) Để độ cao cực đại bằng với tầm xa của vật, ta cần giải phương trình: hmax = R (v0^2 / 40) = (v0^2 / 10) Với v0^2 khác 0, ta có: 1/40 = 1/10 Điều này là không thể xảy ra, vì vậy không tồn tại góc α để độ cao cực đại bằng với tầm xa của vật