Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi r là bán kính đáy của hình nón, h là độ dài đường cao
Thể tích hình nón là \(\dfrac{1}{3}\pi r^2h\)


*Loại thứ nhất có chiều cao 9cm bao gồm chiều cao của hình nón và bán kính của hình cầu.Mà chiều cao hình nón bằng đường kính hình cầu nên ta có:
2r + r =9 (cm) ⇒ r = 3cm
Chiều cao hình nón là 6cm
Thể tích hình nón:
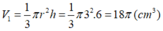
Thể tích nửa hình cầu :
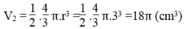
Thể tích loại đồ chơi thứ nhất: V = V 1 + V 2 = 36 π ( c m 3 )
*Loại thứ hai có chiều cao 18cm bao gồm chiều cao của hình nón và bán kính của hình cầu .Mà chiều cao hình nón bằng đường kính hình cầu nên ta có:
2r + r =18 (cm) ⇒ r = 6cm
Chiều cao hình nón là 12cm thể tích hình nón:
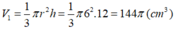
Thể tích nửa hình cầu :
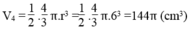
Thể tích loại đồ chơi thứ nhất:
V = V 3 + V 4 = 288 π ( c m 3 )
Vậy t h ể t í c h đ ồ c h ơ i l o ạ i t h ứ h a i t h ể t í c h đ ồ c h ơ i l o ạ i t h ứ n h ấ t = 288 π 36 π =8
Vậy chọn đáp án C

Câu 6:
\(V_1=\dfrac{1}{3}\cdot pi\cdot R^2\cdot h\)
\(V_2=\dfrac{1}{3}\cdot pi\cdot\left(2\cdot R\right)^2\cdot2h=\dfrac{4}{3}\cdot pi\cdot R^2\cdot h\)
=>Thể tích tăng thêm 4 lần

a) Hình cầu bán kính r, vậy thể tích của nó là 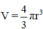
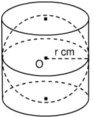
b) Hình trụ có bán kính đáy bằng r và chiều cao bằng 2r
Vậy thể tích của nó là: V 1 = π r 2 ⋅ 2 r = 2 π r 3
c) Thể tích hình trụ trừ đi thể tích hình cầu là:
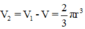
d) Thể tích hình nón có bán kính đáy r, chiều cao 2r
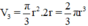
e) Từ các kết quả trên suy ra: Thể tích hình nón "nội tiếp" trong một hình trụ thì bằng thể tích hình trụ trừ đi thể tích hình cầu nội tiếp trong hình trụ ấy.
Hoặc: Thể tích hình trụ bằng tổng thể tích hình nón và hình cầu nội tiếp hình trụ.

Thể tích đồ chơi loại thứ nhất là 36 π ( c m 3 )
Vậy chọn đáp án B

Lời giải:
Gọi bán kính đáy khúc gỗ là $r$ (cm) thì:
Thể tích khúc gỗ:
$\pi r^2h=15\pi r^2$ (cm khối)
Thể tích hình nón:
$\frac{1}{3}\pi r^2h=5\pi r^2$ (cm khối)
Thể tích phần bỏ đi:
$15\pi r^2-5\pi r^2=640r$ (cm khối)
$10\pi r^2=640r$
$10\pi r=640$
$r=\frac{64}{\pi}$ (cm)
Thể tích khối nón: $5\pi r^2=5\pi.\frac{64^2}{\pi ^2}=\frac{20480}{\pi}$ (cm khối)
Nghe đề bài có vẻ sai sai. Nếu đề là $640\pi$ (cm khối) thì bạn cũng làm tương tự, $r=8$ (cm)
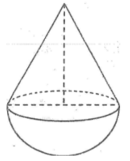

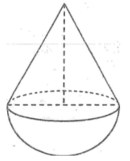

Gọi r và h lần lượt là bán kính đáy và độ dài đường cao hình nón
Thể tích hình nón :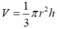
Vậy chọn đáp án D