Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: M(x)=5x^4+4x^3+2x+1-5x^4+x^3+3x^2+x-1
=5x^3+3x^2+3x
b: N(x)=5x^4+4x^3+2x+1+5x^4-x^3-3x^2-x+1
=10x^4+3x^3-3x^2+x+2
`@` `\text {dnammv}`
` \text {M(x)-A(x)=B(x)}`
`-> \text {M(x)=A(x)+B(x)}`
`-> M(x)=(5x^4 + 4x^3 + 2x + 1)+(-5x^4 + x^3 + 3x^2 + x - 1)`
`= 5x^4 + 4x^3 + 2x + 1-5x^4 + x^3 + 3x^2 + x - 1`
`= (5x^4-5x^4)+(4x^3+x^3)+3x^2+(2x+x)+(1-1)`
`= 5x^3+3x^2+3x`
`b,`
`\text {N(x)=A(x)-B(x)}`
`N(x)=(5x^4 + 4x^3 + 2x + 1)-(-5x^4 + x^3 + 3x^2 + x - 1)`
`= 5x^4 + 4x^3 + 2x + 1+5x^4 - x^3 - 3x^2 - x + 1`
`= (5x^4+5x^4)+(4x^3-x^3)-3x^2+(2x-x)+(1+1)`
`= 10x^4+3x^3-3x^2+x+2`

Ta có:
f(x) = -15x3 + 5x4 - 4x2 + 8x2 - 9x3 - x4 + 15 - 7x3
= (5x4 - x4) - (15x3 + 9x3 + 7x3) + (-4x2 + 8x2) + 15
= 4x4 - 31x3 + 4x2 + 15

f(1) = 4.14 - 31.13 + 4.12 + 15 = 4 - 31 + 4 + 15 = -8
f(-1) = 4.(-1)4 - 31.(-1)3 + 4.(-1)2 + 15 = 4 + 31 + 4 + 15 = 54

Ta đặt và thực hiện các phép tính P(x) + Q(x) và P(x) – Q(x).

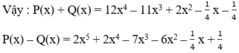

b)
Sửa đề: f(x)=A(x)+B(x)
Ta có: f(x)=A(x)+B(x)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)
\(=12x^4-11x^3+2x^2-\dfrac{1}{4}x-\dfrac{1}{4}\)
a) Ta có: \(A\left(x\right)=x^5-3x^2+7x^4-9x^3+x^2-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3+\left(-3x^2+x^2\right)-\dfrac{1}{4}x\)
\(=x^5+7x^4-9x^3-2x^2-\dfrac{1}{4}x\)
Ta có: \(B\left(x\right)=5x^4-x^5+x^2-2x^3+3x^2-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+\left(x^2+3x^2\right)-\dfrac{1}{4}\)
\(=-x^5+5x^4-2x^3+4x^2-\dfrac{1}{4}\)

`a,`
`P(x)=M(x)+N(x)`
`P(x)=`\(\left(5x^4+8x^2-9x^3-12x-6\right)+\left(-5x^2+9x^3-5x^4+12x-8\right)\)
`P(x)= 5x^4+8x^2-9x^3-12x-6-5x^2+9x^3-5x^4+12x-8`
`P(x)=(5x^4-5x^4)+(-9x^3+9x^3)+(8x^2-5x^2)+(-12x+12x)+(-6-8)`
`P(x)=3x^2-14`
`b,`
`M(x)=N(x)+Q(x)`
`-> Q(x)=M(x)-N(x)`
`-> Q(x)=(5x^4+8x^2-9x^3-12x-6)-(-5x^2+9x^3-5x^4+12x-8)`
`Q(x)=5x^4+8x^2-9x^3-12x-6+5x^2-9x^3+5x^4-12x+8`
`Q(x)=(5x^4+5x^4)+(-9x^3-9x^3)+(8x^2+5x^2)+(-12x-12x)+(-6+8)`
`Q(x)=10x^4-18x^3+13x^2-24x+2`