Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng 2 vận tốc:
210:2=105(km/h)
Vận tốc xe máy:
(105 - 15):2= 45(km/h)
Đ.số: xe máy có vận tốc 45km/h

Gọi vận tốc xe máy là: x (km/h) (Đk: x > 0)
⇒ Vận tốc ô tô là: x + 10 (km/h)
Có: Quãng đường xe máy đi được là \(\dfrac{3x}{4}\left(km\right)\)
Quãng đường ô tô đi được là: \(\dfrac{3\left(x+10\right)}{4}\left(km\right)\)
Theo đầu bài, ta có PT: \(\dfrac{3x}{4}+\dfrac{3\left(x+10\right)}{4}=60\)
\(\Leftrightarrow x=35\left(tm\right)\)
Vậy: Vận tốc xe máy là 35 km/h và vận tốc ô tô là: 35 + 10 = 45 km/h

Xe máy 40km/h
Ô tô 60km/h
Phương trình tg( v1 là vận tốc xe máy thì vận tốc ô tô là v1+20)
(100/2v1+20) + 3/2 = 100/v1
=> 3v12 – 70v1 – 2000 = 0
Gpt đc v1=40 hoặc v1=–16.6666666667(loại)

Gọi vận tốc xe máy là x (km/h). Điều kiện: x > 0
Gọi vận tốc ô tô là y (km/h). Điều kiện: y > 0
Thời gian xe máy dự định đi từ A đến B là: 210/x giờ
Thời gian ô tô dự định đi từ B đến A là: 210/y giờ
Quãng đường xe máy đi được kể từ khi gặp ô tô cho đến khi đến B là: 4x (km)
Quãng đường ô tô đi được kể từ khi gặp xe máy cho đến khi đến A là: 9/4 (km)
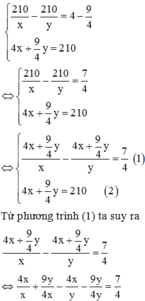
Theo giả thiết ta có hệ phương trình:

Đáp án B

gọi v ô tô là x, v xe máy là y
thời gian 2 xe đi đến C là: 120/x=40/y
=> x=3y
theo đề bài:(40+CD)/x=CD/y
=>CD=20km
=>BD=60km; s ô tô đi = 220km
=>y=60/4=15km/h
x=220/4=55km/h
Gọi vận tốc xe ô tô và xe máy lần lượt là x và y (x,y>0) (km/h)
Ta có : Thời gian ô tô đi quãng đường AC là \(\frac{120}{x}\)
Khi đó, thời gian của xe máy đi quãng đường BC là \(\frac{160-120}{y}=\frac{40}{y}\)
Thời gian xe máy đi quãng đường CD là : \(\frac{CD}{y}\)
Theo đề bài, ta có : \(\frac{CD}{y}=\frac{40+CD}{x}\)
Vì thời gian từ khi khởi hành tới lúc hai xe gặp nhau tại điểm D là 4 giờ nên ta có : \(\frac{40}{y}+\frac{CD}{y}=4\)
Ta có hệ phương trình : \(\hept{\begin{cases}\frac{120}{x}=\frac{40}{y}\left(1\right)\\\frac{CD}{y}=\frac{40+CD}{x}\left(2\right)\\\frac{40}{y}+\frac{CD}{y}=4\left(3\right)\end{cases}}\)
Từ (2) => \(CD=\frac{40}{x-y}.y\) thay vào (3) ta được hệ : \(\hept{\begin{cases}\frac{120}{x}=\frac{40}{y}\\\frac{40}{y}+\frac{40}{x-y}=4\end{cases}}\)\(\Leftrightarrow\)\(\hept{\begin{cases}x=45\\y=15\end{cases}}\) (Thỏa mãn điều kiện)
Vậy vận tốc xe ô tô là 45 km/h
vận tốc xe máy là 15 km/h

Gọi vận tốc của ô tô là x (km/h) (x > 0)
Vì hai xe cùng xuất phát nên khi hai xe gặp nhau thì thời gian đi của hai xe là bằng nhau và khi đó ô tô đi được 75 km còn xe máy đi được 45 km
Thời gian ô tô và xe máy đi cho đến khi gặp nhau là 75/x (h)
Vận tốc của xe máy là: 45 : 75 x = 3 x 5 (km/h)
Nếu xe máy đi trước ô tô 48 phút =4/5 h thì quãng đường đi được của 2 xe bằng nhau và bằng 60km
Thời gian đi quãng đường 60km của ô tô là: 60/x h
Thời gian đi quãng đường 60km của xe máy là: 60 : 3 x 5 = 100 x
Theo bài ra ta có phương trình: 100 x - 60 x = 4 5 ⇔ 40 x = 4 5 ⇔ x = 50 (TM)
Vậy vận tốc của ô tô là 50 km/h, vận tốc của xe máy là 30 km/h
Đáp án: B

V1 Là vận tốc ô tô; t1 là tg v1 đi hết S=210 km
tương tự với v2;...
t' là thời gian gặp nhau
ta có: v1.t1=v2.t2=S;
v1(t'+9/4)=v2(t'+4) => t'+9/4=t1; t'+4=t2;
t'(v1+v2)=v1(t'+9/4) => v1.9/4=t'.v2; tương tự: v2.4=t'.v1
=> 9=t'^2 nên: t'=3.
=> t2=7;t'=21/4 từ đây chia là ra v1;v2.