Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để tính quãng đường vật đi được sau 0,25 s, ta có thể sử dụng phương trình dao động điều hòa x = A * cos(2π/T * t + φ), trong đó x là vị trí của vật (cm), A là biên độ của vật (cm), T là chu kỳ của dao động (s), t là thời gian (s), và φ là góc pha ban đầu (rad).
Trong trường hợp này, phương trình dao động là x = 4cos(4πt + π/4). Ta có thể nhận thấy rằng biên độ của vật là 4 cm và chu kỳ của dao động là T = 1/4 s.
Để tính quãng đường vật đi được sau 0,25 s, ta thay t = 0,25 vào phương trình:
x = 4cos(4π * 0,25 + π/4)
x = 4cos(π + π/4)
x = 4cos(5π/4)
x ≈ 4 * (-0,7071)
x ≈ -2,8284 cm
Vậy, quãng đường vật đi được sau 0,25 s kể từ khi bắt đầu chuyển động là khoảng -2,8284 cm.

Ban đầu vật ở vị trí có pha ban đầu là -pi/3
Sau 13s, vật quét được góc: \(\varphi=\omega t=4\pi.13=52\pi\left(rad\right)\)
Vì góc quay được chia hết cho 2, nghĩa là sau 13s, vật sẽ quay về vị trí ban đầu có pha là -pi/3
\(\Rightarrow S=45cm=3+7.6=\dfrac{A}{2}+7A\)
Vậy vật quay được góc: \(\varphi=\dfrac{\pi}{3}+4\pi-\dfrac{\pi}{2}=\dfrac{23}{6}\pi\left(rad\right)\)
\(\Rightarrow t=\dfrac{\varphi}{\omega}=\dfrac{23\pi}{6.4\pi}=\dfrac{23}{24}\left(s\right)\)

Chọn A
Ta có 5/3 = 3.0,5 + 1/6 = 3T + T/3.
Trong khoảng thời gian T/3 vật đi được quãng đường ngắn nhất là 2.A/2 (khi vật dao động quanh vị trí biên).
→ 3.4A + A = 32,5 ↔ 5A = 32,5 → A = 2,5 cm.

Đáp án D
Ta có 5/3 = 3.0,5 + 1/6 = 3T + T/3.
Trong khoảng thời gian T/3 vật đi được quãng đường ngắn nhất là 2.A/2 (khi vật dao động quanh vị trí biên).
→ 3.4A + A = 32,5 ↔ 5A = 32,5 → A = 2,5 cm
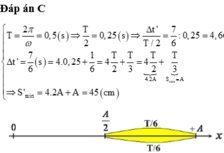


Tham khảo:
\(\left\{{}\begin{matrix}T=\dfrac{2\pi}{\omega}=0,5\left(s\right)\Rightarrow\dfrac{T}{2}=0,25\left(s\right)\Rightarrow\dfrac{\Delta t'}{\dfrac{T}{2}}=\dfrac{7}{6}:0,25=4,6\\\Delta t'=\dfrac{7}{6}\left(s\right)=4\cdot0,25+\dfrac{1}{6}=4\dfrac{T}{2}+\dfrac{T}{3}\\\Rightarrow S'_{min}=4\cdot2A+A=45\left(cm\right)\end{matrix}\right.\)