Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số sách ngăn thứ hai là x thì số ngăn sách ngăn thứ nhất là 2x (x>0)
Nếu chuyển 15 cuốn ngăn thứ nhất sang ngăn thứ hai thì số sách ở ngăn thứ hai bằng 8/7 số sách ở ngăn thứ nhất nên ta có PT:
\(\frac{2x-15}{x+15}=\frac{7}{8}\) \(\Leftrightarrow\) 16x-120=7x+105 \(\Leftrightarrow\) 9x=225 \(\Leftrightarrow\) x=25 (thỏa mãn ĐK)
Vậy số sách ở ngăn thứ nhất là 50 và số sách ở ngăn thứ hai là 25

Gọi số sách ban đầu ở ngăn thứ 2 là x>0 cuốn
\(\Rightarrow\) Số sách ban đầu ở ngăn 1 là \(3x\)
Sau khi chuyển, số sách ở ngăn 1 là: \(3x-15\)
Số sách ngăn 2 là: \(x+15\)
Theo bài ra ta có pt:
\(3x-15=x+15\)
\(\Leftrightarrow2x=30\Rightarrow x=15\)
Vậy ban đầu ngăn 1 có 45 cuốn, ngăn 2 có 15 cuốn
Gọi số sách ngăn thứ 2 là x (quyển, x>0)
=> số sách ngăn thứ nhất: 3x (quyển)
Theo bài ta có :
3x - 15 = x + 15
=> 2x = 30
=> x = 15 (tmx>0)
Vậy số sách ngăn thứ nhất là 15 quyển, ngăn thứ hai là 15.3 = 45 quyển

Gọi số cần tìm là \(\overline{ab}\) theo đề bài
\(\overline{ba}-\overline{ab}=27\Rightarrow10b+a-10a-b=27\)
\(\Rightarrow9b-9a=27\Rightarrow b-a=3\) mà \(a+b=9\)
\(\Rightarrow b=6;a=3\)

Lời giải:
Gọi số cần tìm là $\overline{ab}$ với $a,b$ là STN và $0\leq a,b\leq 9;a\neq 0$.
Theo bài ra ta có:
$\overline{1ab}=5\overline{ab}$
$\Leftrightarrow 100+\overline{ab}=5\overline{ab}$
$\Leftrightarrow 100=4\overline{ab}$
$\Leftrightarrow 25=\overline{ab}$
Vậy số cần tìm là $25$

Gọi x là, số nhà bạn Khanh. Điều kiện: x ∈N* và 9 < x < 100.
Thêm số 5 vào bên trái số nhà bạn Khanh ta được:
A = 5 x ¯ = 500 + x
Thêm số 5 vào bên phải số nhà bạn Khanh ta được:
B = x 5 ¯ = 10x + 5
Vì hiệu của A - B = 153 nên ta có phương trình:
(500 + x) - (10x + 5) = 153 ⇔ 500 + x - 10x - 5 = 153
⇔ - 9x = 153 – 500 + 5 ⇔ - 9x = - 342 ⇔ x = 38 (thỏa mãn)
Vậy số nhà bạn Khanh là 38.

Gọi số tự nhiên có hai chữ số cần tìm là 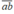 = 10a + b (a, b ∈ N,0 < a ≤ 7, 0 ≤ b < 7)
= 10a + b (a, b ∈ N,0 < a ≤ 7, 0 ≤ b < 7)
Ta có a + b = 7 .
Khi thêm chữ số 0 vào giữa ta được số 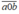 = 100a + b
= 100a + b
Vì số mới hơn số đã cho 180 nên ta có phương trình:
100a + b = 10a + b + 180
⇔ 90a = 180
⇔ a = 2 (tmđk)
⇒ b = 7- a = 5
Vậy số tự nhiên có hai chữ số cần tìm là 25.

Gọi chữ số hàng chục là a thì chữ số hàng đơn vị là 7 - a
Thêm chữ số vào giữa 2 chữ số ta được số mới là: a0(7-a)
Ta có phương trình:
\(\overline{a0\left(7-a\right)}\)\(-\)\(\overline{a\left(7-a\right)}\)\(=180\)
\(\Leftrightarrow\)\(100a+\left(7-a\right)-10a-\left(7-a\right)=180\)
\(\Leftrightarrow\)\(90a=180\)
\(\Leftrightarrow\)\(a=2\)
Vậy chữ số hàng chục là 2
Chữ số hàng đơn vị là: \(7-2=5\)
Vậy số cần tìm là: \(25\)
Số sách nhà văn đó đã viết : 99^2 = 9801 (cuốn sách)