Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có x ∈ (0; 60000)
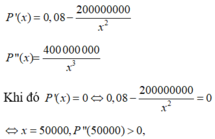
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C

Lời giải:
Theo bài ra ta có \(m^{\frac{2}{3}}n^{\frac{1}{3}}\geq 40\Rightarrow m^2n\geq 40^3\)
Số chi phí phải trả mỗi ngày là:
\(P=6m+24n\). Ta cần tìm min \(P\)
Áp dụng BĐT Cauchy ta có:
\(P=3m+3m+24n\geq 3\sqrt[3]{3m.3m.24n}=3\sqrt[3]{216m^2n}\geq 3\sqrt[3]{216.40^3}=720\)
Vậy \(P_{\min}=720(\text{USD})\) tức là chi phí ít nhất mỗi ngày phải trả là \(720 (\text{USD})\)

10987+9876+8765+7654+5432+4321=6899.9877.9876.9999 tôi ko biết bài tôi vừa làm mà đúng hay là sai

a)
Xác suất lấy được phế phẩm:
\(H=35\%.1\%+40\%.1,5\%+0,8\%.25\%=1,15\%\)
b) Sp máy I: 35%.1%= 0,35%
Sp máy 2: 40%.1,5%= 0,6%
Sp máy 3: 0,8%.25%=0,2%
=> Kết luận...(Em tự so sánh nè)


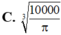
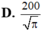

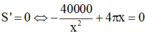
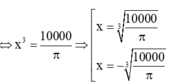
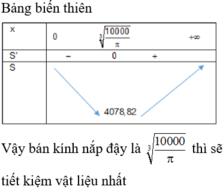

Trong 1 ngày nhà máy đó sản xuất được số chiếc ti vi là
680 : 4 = 170 (chiếc)
Trong 7 ngày nhà máy đó sản xuất được số chiếc ti vi
170 x 7 = 1190(chiếc)
Đáp số : 1190 chiếc tivi
HT
1 ngày sản xuất đc là :
680:4=170(tivi)
7 ngày sản xuất là:
170*7=840(tivi)
đáp số:840 tivi