Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có x ∈ (0; 60000)
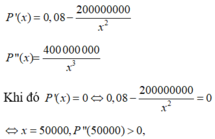
Do đó, hàm số đạt cực tiểu tại x = 50000.
Nên x=50000 là số sản phẩm cần sản xuất mỗi ngày để tối thiểu chi phí.
Chọn C

Chọn A.
Gọi x; y lần lượt là số phẩm loại A; B.
Theo đề bài ta có: 2000x + 4000y = 40 000 hay x + 2y = 20
Suy ra: x = 20 - 2y.
Ta có ![]()
Xét hàm ![]()
Tập xác định D = (0; 10).
![]()
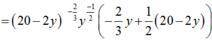
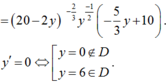
Nhận xét: ![]() nên dấu của y’ là dấu của biểu thức
nên dấu của y’ là dấu của biểu thức ![]()
Do đó hàm số đạt giá trị lớn nhất khi y = 6 và x = 8
Vậy ![]()

Gọi chiều rộng đáy của thùng hàng là x (x>0)
Chiều dài: \(\dfrac{3}{2}x\)
Chiều cao: \(\dfrac{15}{x.\dfrac{3}{2}x}=\dfrac{10}{x^2}\)
Diện tích đáy : \(\dfrac{3}{2}x^2\)
Diện tích mặt bên: \(2x.\dfrac{10}{x^2}+3x.\dfrac{10}{x^2}=\dfrac{50}{x}\)
Tổng chi phí: \(f\left(x\right)=10.\dfrac{3}{2}x^2+6.\dfrac{50}{x}=15x^2+\dfrac{300}{x}\)
\(f\left(x\right)=15\left(x^2+\dfrac{20}{x}\right)=15\left(x^2+\dfrac{10}{x}+\dfrac{10}{x}\right)\ge15.3\sqrt[3]{\dfrac{100x^2}{x^2}}\simeq209\left(USD\right)\)
Bạn tính toán lại

Gọi số tiền còn lại phải trả sau i tháng là Pi ; A=300 (triệu) là số tiền đã vay ; d=5,5 (triệu) là số tiền trả cố định tháng ; r=0,5% là lãi trên tháng
Ta luôn có, tại thời điểm tháng thứ i, số tiền còn lại phải trả là Pi bằng số tiền còn lại phải trả của tháng trước đó trừ đi tiền lãi ( Pi-1*r ) và trừ thêm tiền trả cố định hàng tháng (d) ; viết gọn lại là \(P_i=P_{i-1}-P_{i-1}\cdot r-d=P_{i-1}\left(1-r\right)-d\)
Áp dụng côn thức trên ta có:
Ngay tại thời điểm vay xong thì \(P_0=A\)
qua tháng thứ nhất : \(P_1=P_0-P_0r-d=A\left(1-r\right)-d\)
qua tháng thứ hai : \(P_2=P_1\left(1-r\right)-d=A\left(1-r\right)^2-d\cdot\left[\left(1-r\right)+1\right]\)
.....
qua tháng thứ k : \(P_k=P_{k-1}\left(1-r\right)-d=A\left(1-r\right)^k-d\cdot\left[\left(1-r\right)^{k-1}+\left(1-r\right)^{k-2}+...+\left(1-r\right)+1\right]\\ =A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}\)
Xét thời điểm trả hết nợ, tức là Pk=0
\(\Leftrightarrow A\left(1-r\right)^k-d\cdot\frac{\left(1-r\right)^k-1}{\left(1-r\right)-1}=0\\ \Leftrightarrow300\left(1-0,5\%\right)^k=5,5\cdot\frac{\left(1-0,5\%\right)^k-1}{\left(1-0,5\%\right)-1}\\ \Leftrightarrow\left(1-0,5\%\right)^k=\frac{11}{14}\Leftrightarrow k\approx48,1117\)
Bạn nhớ luôn công thức tren để giải bài tập liên quan nhé

a)
Xác suất lấy được phế phẩm:
\(H=35\%.1\%+40\%.1,5\%+0,8\%.25\%=1,15\%\)
b) Sp máy I: 35%.1%= 0,35%
Sp máy 2: 40%.1,5%= 0,6%
Sp máy 3: 0,8%.25%=0,2%
=> Kết luận...(Em tự so sánh nè)



Lời giải:
Theo bài ra ta có \(m^{\frac{2}{3}}n^{\frac{1}{3}}\geq 40\Rightarrow m^2n\geq 40^3\)
Số chi phí phải trả mỗi ngày là:
\(P=6m+24n\). Ta cần tìm min \(P\)
Áp dụng BĐT Cauchy ta có:
\(P=3m+3m+24n\geq 3\sqrt[3]{3m.3m.24n}=3\sqrt[3]{216m^2n}\geq 3\sqrt[3]{216.40^3}=720\)
Vậy \(P_{\min}=720(\text{USD})\) tức là chi phí ít nhất mỗi ngày phải trả là \(720 (\text{USD})\)